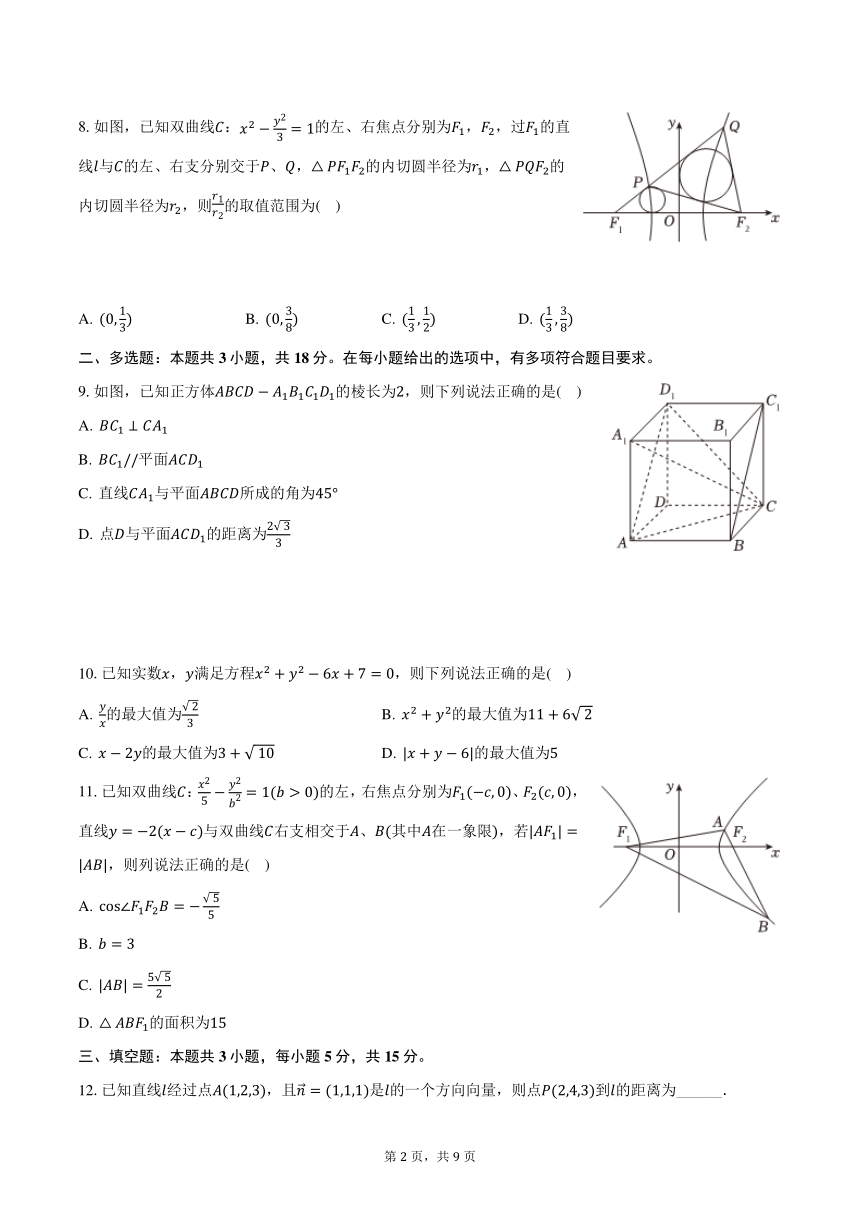
重庆市鲁能巴蜀中学2024-2025学年高二上学期期中考试数学试卷(PDF版，含答案)

重庆市鲁能巴蜀中学 2024-2025 学年高二上学期期中考试数学试卷 一、单选题：本题共 8 小题，每小题 5 分，共 40 分。在每小题给出的选项中，只有一项是符合题目要求的。 1.直线 1： = √ 3 + 1与 2： + 1 = 0互相垂直，则实数 =( ) √ 3 √ 3 A. √ 3 B. √ 3 C. D. 3 3 2.已知空间中，点 (1,2, 1)， ( 2,1, 1)， ( 1,2,0)，则平面 的一个法向量为( ) A. (2,1,3) B. (1, 3,2) C. (1,3,2) D. ( 1,2,2) 11 3.若直线 ： + √ 2 = 0与圆 ：( √ 2)2 + 2 = 交于 ， 两点，则| | =( ) 3 A. 1 B. √ 3 C. 2 D. 2√ 3 1 4.抛物线 = 2上一点 到 (0,2)的距离的最小值为( ) 2 A. 1 B. √ 2 C. √ 3 D. 2 5.已知圆 1：( + 3) 2 + 2 = 100和 ：( 3)2 22 + = 4，若动圆 与这两圆一个内切一个外切，记该动 圆圆心的轨迹为 ，则 的方程为( ) 2 2 2 2 2 2 2 2 A. + = 1 B. + = 1 C. + = 1 D. + = 1 36 27 36 9 25 16 25 9 6.如图，在平行六面体 1 1 1 1中，∠ = 90°，∠ 1 = ∠ 1 = 60°， = = 1 = 2，则异面直线 1 与 1 1所成角的余 弦值为( ) √ 6 √ 6 √ 6 √ 6 A. B. C. D. 6 6 3 3 7.如图，曲线 由三部分构成：半圆 1：( + 1) 2 + 2 = 1( ≥ 0)，半圆 2： 2 2 ( 1)2 3 + 2 = 1( ≥ 0)，半椭圆 ： + = 1( < 0)，直线 ： = ( 4 3 4 1)交 于 、 ，动点 在曲线 上，则△ 面积的最大值为( ) 21 77 11 A. B. C. D. 4 10 20 4 第 1 页，共 9 页 2 8.如图，已知双曲线 ： 2 = 1的左、右焦点分别为 1， 2，过 1的直3 线 与 的左、右支分别交于 、 ，△ 1 2的内切圆半径为 1，△ 2的 1 内切圆半径为 2，则 的取值范围为( ) 2 1 3 1 1 1 3 A. (0, ) B. (0, ) C. ( , ) D. ( , ) 3 8 3 2 3 8 二、多选题：本题共 3 小题，共 18 分。在每小题给出的选项中，有多项符合题目要求。 9.如图，已知正方体 1 1 1 1的棱长为2，则下列说法正确的是( ) A. 1 ⊥ 1 B. 1//平面 1 C. 直线 1与平面 所成的角为45° 2√ 3 D. 点 与平面 1的距离为 3 10.已知实数 ， 满足方程 2 + 2 6 + 7 = 0，则下列说法正确的是( ) √ 2 A. 的最大值为 B. 2 + 2的最大值为11 + 6√ 2 3 C. 2 的最大值为3 + √ 10 D. | + 6|的最大值为5 2 2 11.已知双曲线 ： 2 = 1( > 0)的左，右焦点分别为 1( , 0)、 2( , 0)，5 直线 = 2( )与双曲线 右支相交于 、 (其中 在一象限)，若| 1| = | |，则列说法正确的是( ) √ 5 A. cos∠ 1 2 = 5 B. = 3 5√ 5 C. | | = 2 D. △ 1的面积为15 三、填空题：本题共 3 小题，每小题 5 分，共 15 分。 12.已知直线 经过点 (1,2,3)，且 = (1,1,1)是 的一个方向向量，则点 (2,4,3)到 的距离为_____． 第 2 页，共 9 页 13.已知抛物线 ： 2 = 2 ( > 0)，直线 = 1与抛物线相交于 、 ，且 的中点为 (2,2)，则 = _____． 14.平面点集{( , )|( )2 + ( )2 = 25， ∈ }所构成区域的面积为_____． 四、解答题：本题共 5 小题，共 77 分。解答应写出文字说明，证明过程或演算步骤。 15.(本小题13分) 已知圆 1： 2 + 2 6 + 2 + 2 + 8 = 0，圆 2 22： + = 16，直线 ： = 5( > 0)． (1)若圆 1与圆 2外切，求实数 的值； (2)若 与圆 1、 2都相切，求实数 的值． 16.(本小题15分) √ 6 2√ 6 已知椭圆 经过点 (√ 2, )， ( , 1)． 2 3 (1)求椭圆 的方程； (2)设椭圆 的左右焦点分别为 1、 2，过点 1且斜率为 的直线 与椭圆 交于 、 两点，若∠ 2 为锐角， 求 的取值范围． 17.(本小题15分) 1 如图，在四棱锥 中， = = = = = 2， // ，∠ = ∠ = 90°，平面 ⊥ 2 平面 ， 为 中点． (1)求证： ⊥面 ； √ 5 (2)点 在棱 上，设 = (0 < < 1)，若二面角 余弦值为 ，求 ． 5 18.(本小题17分) 2 2 已知双曲线 ： 2 2 = 1( > 0, > 0)的左、右焦点为 1( , 0)、 2( , 0)，直线 1： ... ...