第四章 图形的平移与旋转 2 图形的旋转 第3课时 旋转对称图形(含答案)

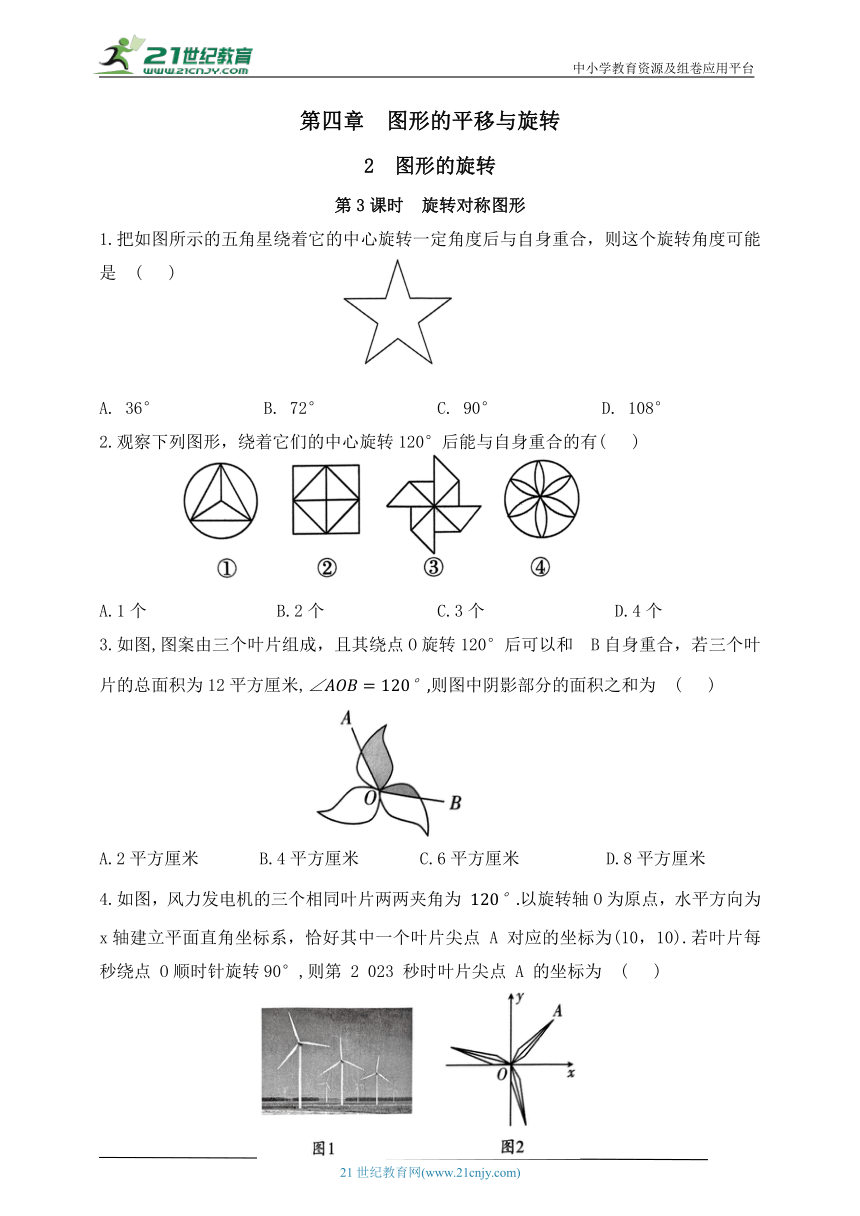
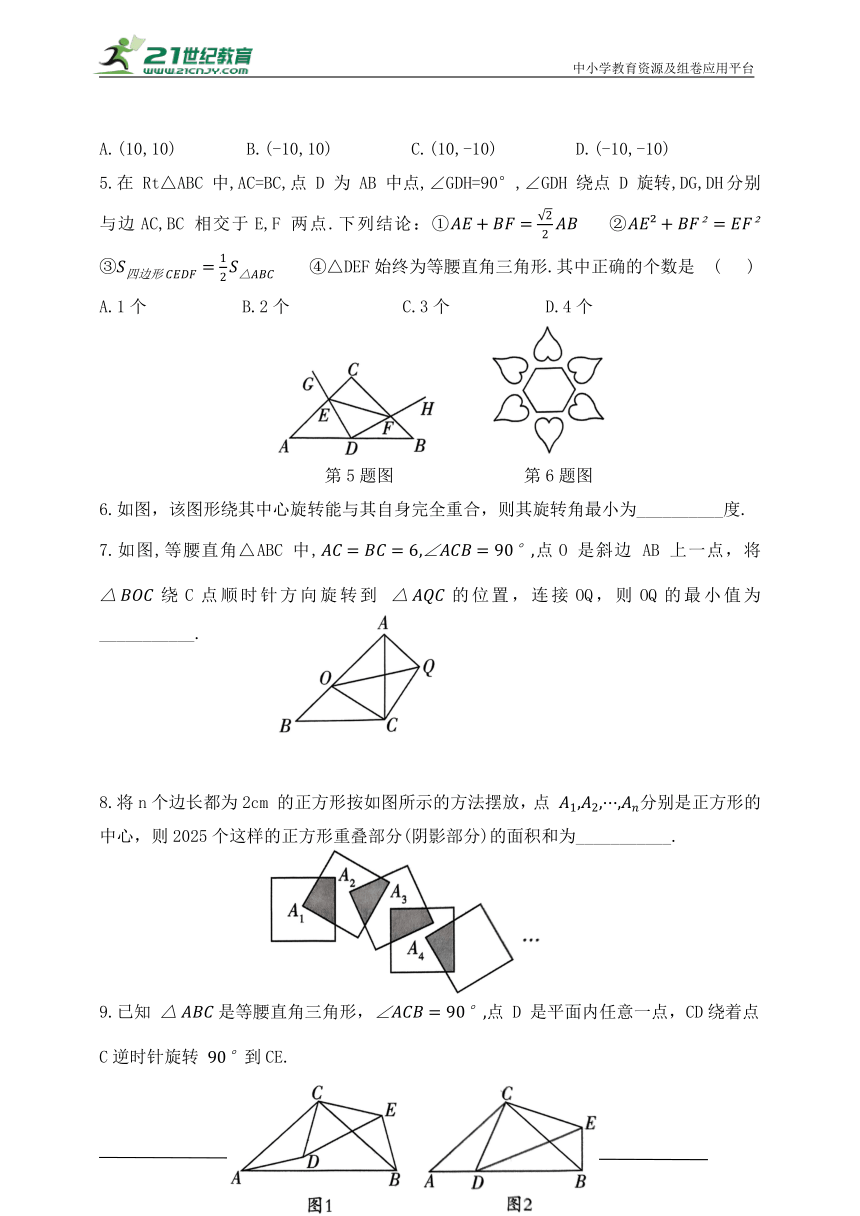
中小学教育资源及组卷应用平台 第四章 图形的平移与旋转 2 图形的旋转 第3课时 旋转对称图形 1.把如图所示的五角星绕着它的中心旋转一定角度后与自身重合，则这个旋转角度可能是 ( ) A. 36° B. 72° C. 90° D. 108° 2.观察下列图形，绕着它们的中心旋转120°后能与自身重合的有( ) A.1个 B.2个 C.3个 D.4个 3.如图,图案由三个叶片组成，且其绕点O旋转120°后可以和 B自身重合，若三个叶片的总面积为12平方厘米,则图中阴影部分的面积之和为 ( ) A.2平方厘米 B.4平方厘米 C.6平方厘米 D.8平方厘米 4.如图，风力发电机的三个相同叶片两两夹角为 以旋转轴O为原点，水平方向为x轴建立平面直角坐标系，恰好其中一个叶片尖点 A 对应的坐标为(10，10).若叶片每秒绕点 O顺时针旋转90°,则第 2 023 秒时叶片尖点 A 的坐标为 ( ) A.(10,10) B.(-10,10) C.(10,-10) D.(-10,-10) 5.在 Rt△ABC 中,AC=BC,点 D 为 AB 中点,∠GDH=90°,∠GDH 绕点 D 旋转,DG,DH分别与边AC,BC 相交于E,F 两点.下列结论：① ② ④△DEF始终为等腰直角三角形.其中正确的个数是 ( ) A.1个 B.2个 C.3个 D.4个 第5题图 第6题图 6.如图，该图形绕其中心旋转能与其自身完全重合，则其旋转角最小为_____度. 7.如图,等腰直角△ABC 中,点O 是斜边 AB 上一点，将绕C点顺时针方向旋转到 的位置，连接OQ，则OQ的最小值为_____. 8.将n个边长都为2cm 的正方形按如图所示的方法摆放，点 分别是正方形的中心，则2025个这样的正方形重叠部分(阴影部分)的面积和为_____. 9.已知 是等腰直角三角形，点 D 是平面内任意一点，CD绕着点C逆时针旋转 到CE. (1)如图1,若 D 为 内一点，求证： (2)如图2,若 D 为 AB 边上一点, 求 DE 的长. 10.(1)如图1,O是等边 内一点，连接OA,OB,OC,且OA=3,OB=4,OC=5,将绕点 B 顺时针旋转后得到△BCD,连接OD. 求：①旋转角的度数为_____； ②线段OD的长_____; ③求∠BDC的度数; (2)如图 2 所示，O是等腰直角 内一点,连接OA,OB,OC,将 绕 点 B 顺时针旋转后得到连接OD.当OA,OB,OC 满足什么条件时，请给出证明. 11.如图,在平面直角坐标系中，将△ABO绕点A 顺时针旋转到△AB C 的位置,点 B,O分别落在点 B ,C 处,点 B 在x轴上；再将△AB C 绕点 B 顺时针旋转到△A B C 的位置,点 C 在x轴上,将△A B C 绕点 C 顺时针旋转到△A B C 的位置,点 A 在x轴上,…,若点 A(2,0),点 B(0,3),则 B 的坐标是 ( ) 参考答案 1. B 2. B 3. B 4. B 5. D 6. 60 7. 6 8. 2024 cm 9.解:(1)证明:∵△ABC 是等腰直角三角形,∠ACB=90°,∴AC=BC, ∵CD绕着点C 逆时针旋转90°到 CE,∴∠DCE=90°,CD=CE, ∴∠ACB-∠DCB=∠DCE-∠DCB,即∠ACD=∠BCE. 在△ACD 和△BCE中, ∴△ACD≌△BCE(SAS),∴AD=BE; (2)∵△ABC是等腰直角三角形,∴∠A=∠ABC=45°. ∵△ACD≌△BCE,∴∠CBE=∠A=45°,AD=BE, ∴∠ABE=∠ABC+∠CBE=90°, 在 Rt△BDE中,由勾股定理,得 DE , 169,∴DE=13. 10.解:(1)①∵△ABC为等边三角形,∴BA=BC,∠ABC=60°, ∵△BAO绕点 B 顺时针旋转后得到△BCD,∴∠OBD=∠ABC=60°, ∴旋转角的度数为60°； 故答案为:60°; ②∵△BAO 绕点 B 顺时针旋转后得到△BCD,∴BO=BD, 又∵∠OBD=60°,∴△OBD为等边三角形；∴OD=OB=4; 故答案为：4； ③∵△BOD为等边三角形,∴∠BDO=60°, ∵△BAO绕点 B 顺时针旋转后得到△BCD,∴CD=AO=3, 在△OCD中,CD=3,OD=4,OC=5, ∴△OCD 为直角三角形,∠ODC=90°, ∴∠BDC=∠BDO+∠ODC=60°+90°=150°; (2)当 时,∠ODC=90°.理由： ∵△BAO绕点B 顺时针旋转后得到△BCD,∴∠OBD=∠ABC=90°,BO=BD,CD=AO, 为等腰直角三角形， ∵当 时， 为直角三角形， ∴当 OA,OB,OC 满足 时， 11. C 解析:由图象,得点. 在第一象限， …, 当 时， 21世纪教育网 www.21cnjy.com ... ...