相似三角形的性质 同步练习 2024--2025学年初中数学人教版九年级下册

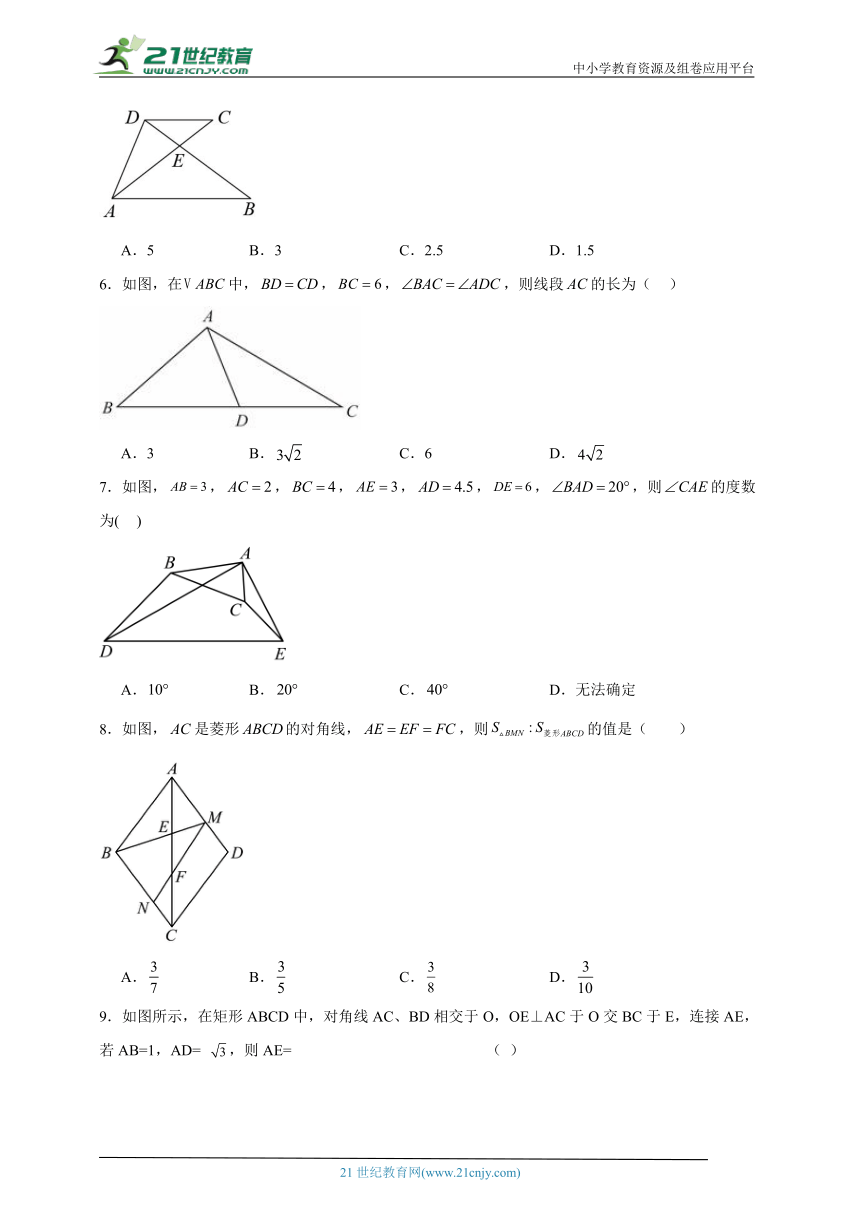
中小学教育资源及组卷应用平台 27.2.2相似三角形的性质 同步练习 2024--2025学年初中数学人教版九年级下册 一、单选题 1．已知，△ABC∽△DEF，△ABC与△DEF的面积之比为1：2，当BC=1，对应边EF的长是（ ） A． B．2 C．3 D．4 2．已知△ABC∽△DEF，如果∠A=55 ，∠B=100 ，则∠F=（ ） A．55 B．100 C．25 D．30 3．如图，，，与的面积分别是与，周长分别是与，则下列说法正确的是（ ） A． B． C． D． 4．如图，在△ABC中，点E，F分别在边AC，BC上，EF∥AB．若CE＝2AE，AB＝4，则EF的长为（　　） A． B．1 C．2 D． 5．如图，AC、BD交于点E，若//CD，，，则△ADE的面积的值是（ ） A．5 B．3 C．2.5 D．1.5 6．如图，在中，，，，则线段的长为（ ） A．3 B． C．6 D． 7．如图，，，，，，，，则的度数为( ) A． B． C． D．无法确定 8．如图，是菱形的对角线，，则的值是（　　） A． B． C． D． 9．如图所示，在矩形ABCD中，对角线AC、BD相交于O，OE⊥AC于O交BC于E，连接AE，若AB=1，AD= ，则AE= （ ） A． B． C． D．2 10．如图，在△ABC 中，∠C=90°，BC=6，D，E 分别在 AB、AC上，将△ABC沿DE折叠，使点A落在点A′处，若A′为CE的中点，则折痕DE的长为（　　） A． B．2 C．3 D．4 二、填空题 11．如果两个相似三角形的面积比为1:4，其中较大三角形的周长为18，那么较小三角形的周长是 ． 12．如图，点是边上一点，若，，，则 ． 13．如图，在△ABD中，C为AD上一点，AB＝CD＝1，∠ABC＝90°，∠CBD＝30°，则AC＝ ． 14．如图，正方形ABCD的边长为1cm，M、N分别是BC、CD上两个动点，且始终保持AM⊥MN，则△ADN的最小面积为 ． 15．如图，在△ABC中，DE∥BC，AC＝4，AB＝3，EC＝1，则AD= ，BD= ． 16．如图，AD是△ABC中BC边上的中线，点G是△ABC的重心，AD＝9，DG＝ ． 三、解答题 17．如图，在中，，求的长度． 18．如图，为了估算河的宽度，我们可以在河对岸选定一个目标点A，在近岸取点和点，观察者在点．适当调整，使得与都与河岸垂直．此时与相交于点，若测得，，请利用这些数据计算河的宽度． 19．如图，在7×7的正方形网格中，点A，B均在格点上，请你借助格点，仅用无刻度的直尺按要求作图．（保留作图痕迹） 　　　　　图1　　　　　　　　　图2 (1)如图1，作出线段AB的中点P． (2)如图2，作出线段AB的三等分点Q． 20．在平行四边形ABCD中，M，N为对角线BD的三等分点，连接AM交BC于E，连接EN并延长交AD于F． （1）试说明△AMD∽△EMB； （2）求的值． 参考答案 1．A 解：∵△ABC∽△DEF，△ABC与△DEF的面积之比为1：2， ∴， 解得BC：EF=1：， ∵BC=1， ∴EF=． 2．C ∵△ABC∽△DEF，∴∠A=∠D，∠B=∠E，∠C=∠F，已知∠A=55°，∠B=100°， ∴∠C=∠F=180°-∠A-∠B=180°-55°-100°=25°．故选C. 3．A 解：∵，， ∴，A正确，符合题意； ∴，B错误，不符合题意； ∵和不是对应边， ∴不一定等于，C错误，不符合题意； ∴，D错误，不符合题意； 4．A 解:∵EF∥AB，CE＝2AE， ∴△CEF∽△CAB， ∴＝＝， ∵AB＝4， ∴EF＝ ． 5．C 解：∵//CD， ∴， ， ， ， ， ：， ， 6．B 解：∵，， ∴， ∵，， ∴△ABC∽△DAC， ∴，即， ∴， ∴； 7．B 解：∵，，， ∴， ∴△ABC∽△ADE， ∴∠BAC=∠DAE， ∴∠CAE=∠BAD=. 8．C 解：如图，连接， ∵四边形是菱形， ∴，， ∴，， ∴， ∵， ∴， ∴， ∴， ∴， ∴． 9．C 在直角△ABC中，BC=AD=，AB=1 ∴AC=2 ∴OA=OC=1 ∵∠EOC=∠ABC=90°，∠OCE=∠BCA ∴△COE∽△CBA ∴ ∴OE= 在直角△OAE中，AE= 10．B ∵△ABC沿DE折叠，使点A落在点A′处， ∴∠DEA=∠DEA′=90°，AE=A′E， ∴DE∥BC ∴△ACB∽△AED， 又A′为CE的中点， ∴AE=A'E=A'C=AC， ∴， ... ...