第七章 相交线与平行线 问题解决活动：折平行线 同步练习(含答案)

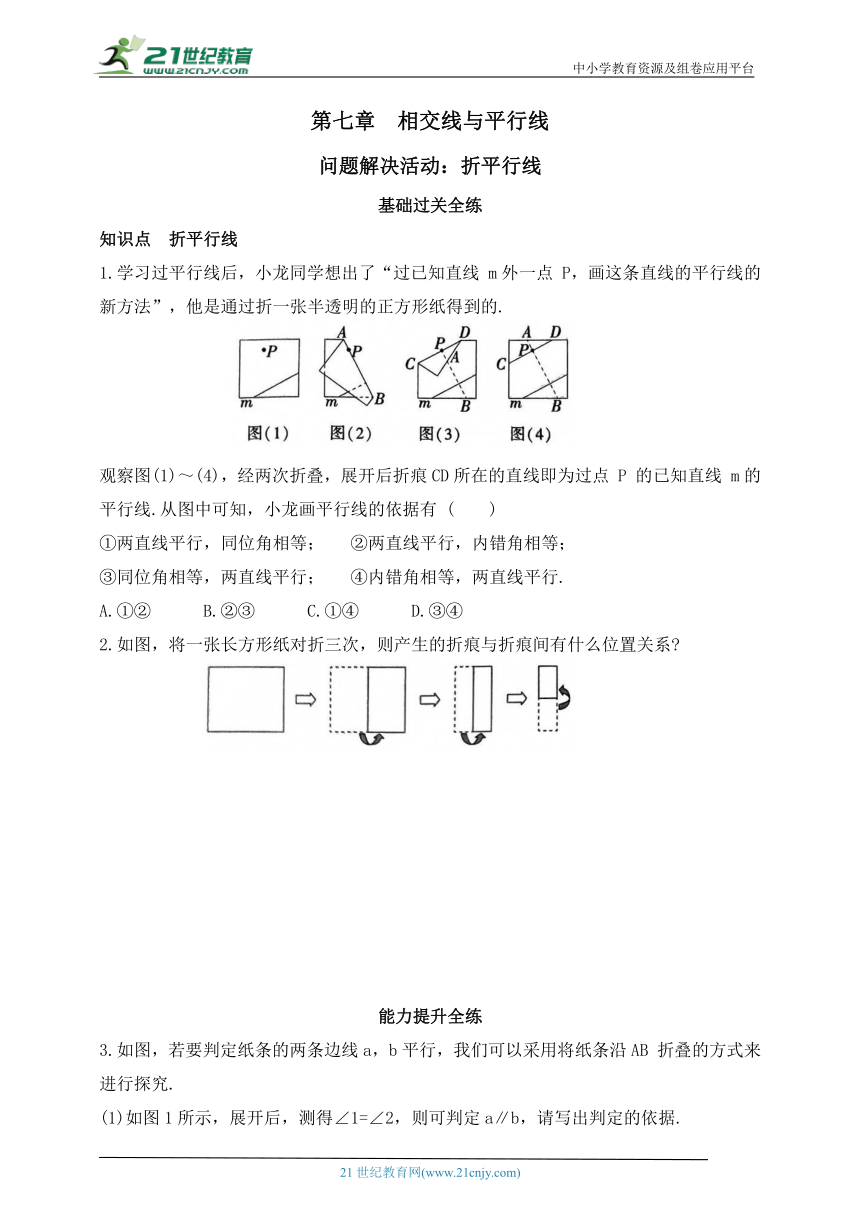
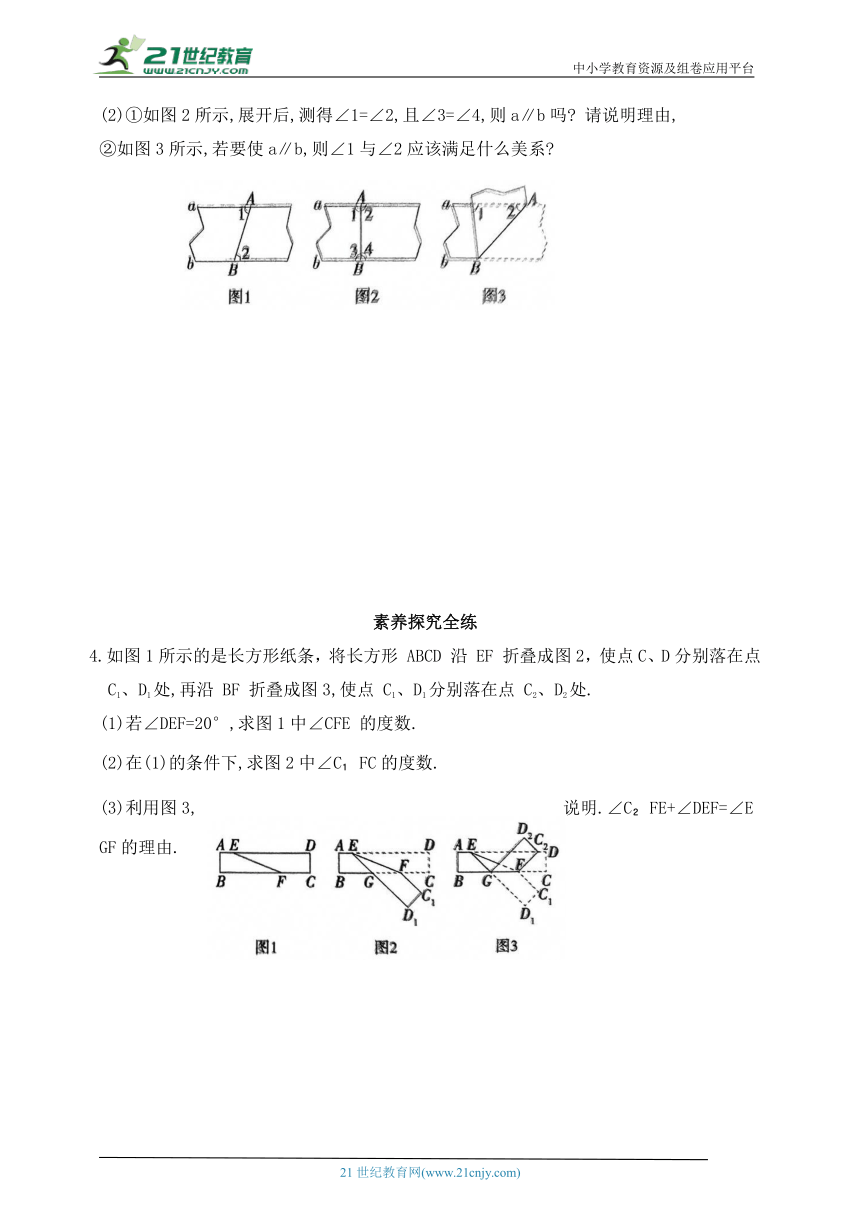
中小学教育资源及组卷应用平台 第七章 相交线与平行线 问题解决活动：折平行线 基础过关全练 知识点 折平行线 1.学行线后，小龙同学想出了“过已知直线 m外一点 P，画这条直线的平行线的新方法”，他是通过折一张半透明的正方形纸得到的. 观察图(1)～(4)，经两次折叠，展开后折痕CD所在的直线即为过点 P 的已知直线 m的平行线.从图中可知，小龙画平行线的依据有 ( ) ①两直线平行，同位角相等； ②两直线平行，内错角相等； ③同位角相等，两直线平行； ④内错角相等，两直线平行. A.①② B.②③ C.①④ D.③④ 2.如图，将一张长方形纸对折三次，则产生的折痕与折痕间有什么位置关系 能力提升全练 3.如图，若要判定纸条的两条边线a，b平行，我们可以采用将纸条沿AB 折叠的方式来进行探究. (1)如图1所示，展开后，测得∠1=∠2，则可判定a∥b，请写出判定的依据. (2)①如图2所示,展开后,测得∠1=∠2,且∠3=∠4,则a∥b吗 请说明理由, ②如图3所示,若要使a∥b,则∠1与∠2应该满足什么美系 素养探究全练 4.如图1所示的是长方形纸条，将长方形 ABCD 沿 EF 折叠成图2，使点C、D分别落在点 C1、D1处,再沿 BF 折叠成图3,使点 C1、D1分别落在点 C2、D2处. (1)若∠DEF=20°,求图1中∠CFE 的度数. (2)在(1)的条件下,求图2中∠C FC的度数. (3)利用图3,说明.∠C FE+∠DEF=∠EGF的理由. 参考答案 基础过关全练 1.D 第一次折叠后，得到的折痕AB 与直线 m 之间的位置关系是垂直；将正方形纸展开，再进行第二次折叠，得到的折痕CD 与第一次的折痕AB 之间的位置关系也是垂直.如图,∵AB⊥m,CD⊥AB,∴∠1=∠2=∠3=∠4=90°,∵∠3=∠1,∴m∥CD(同位角相等,两直线平行),故③符合.∵∠4=∠2,∴m∥CD(内错角相等，两直线平行)，故④符合.故选 D. 2.解析 ∵长方形对边平行， ∴根据平行线的传递性，可知前两次折痕互相平行. ∵第三次折叠是把平角折成两个相等的角， ∴ 这两个相等的角都是90°，此折痕与前两次折痕垂直. ∴折痕与折痕之间的位置关系是平行或垂直. 能力提升全练 3.解析 (1)内错角相等，两直线平行. (2)①∵ ∠1 =∠2,∠3=∠4,∠1+∠2= ∠3+∠4=180°, ∴∠1=∠4=90°,∴a∥b. ②如图， 当∠2=∠3时,a∥b. 由翻折的性质可知,∠3=∠4,∴∠2=∠4. ∵∠1+∠2+∠4=180°,∴ ∠1+2∠2=180°. 素养探究全练 4.解析 (1)∵四边形ABCD 是长方形,∴AD∥BC,∴∠DEF+∠CFE=180°. ∵∠DEF=20°, (2)∵四边形 EDCF 折叠得到四边形 ED C F, ∵四边形ABCD是长方形,∴AD∥BC, (3)∵四边形ABCD 是长方形,∴AD∥BC,∴∠EFB =∠DEF,∠DEF+∠CFE=180°,∠DEG+∠EGF=180°. 设 ∴ ∠EFB=x°,∠CFE=180°-∠DEF=180°-x°. ∵四边形 EDCF 折叠得到四边形 ED C F,∴∠D EF=∠DEF=x°, ∴ ∠EGF=180°-∠DEG=180°-2x°. ∵ FC ∥ED ,∴∠C FG=∠EGF=180°-2x°. ∵四边形 GD C F折叠得到四边形 GD C F, 180°-3x°, =∠EGF. 21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页） 21世纪教育网(www.21cnjy.com) ... ...