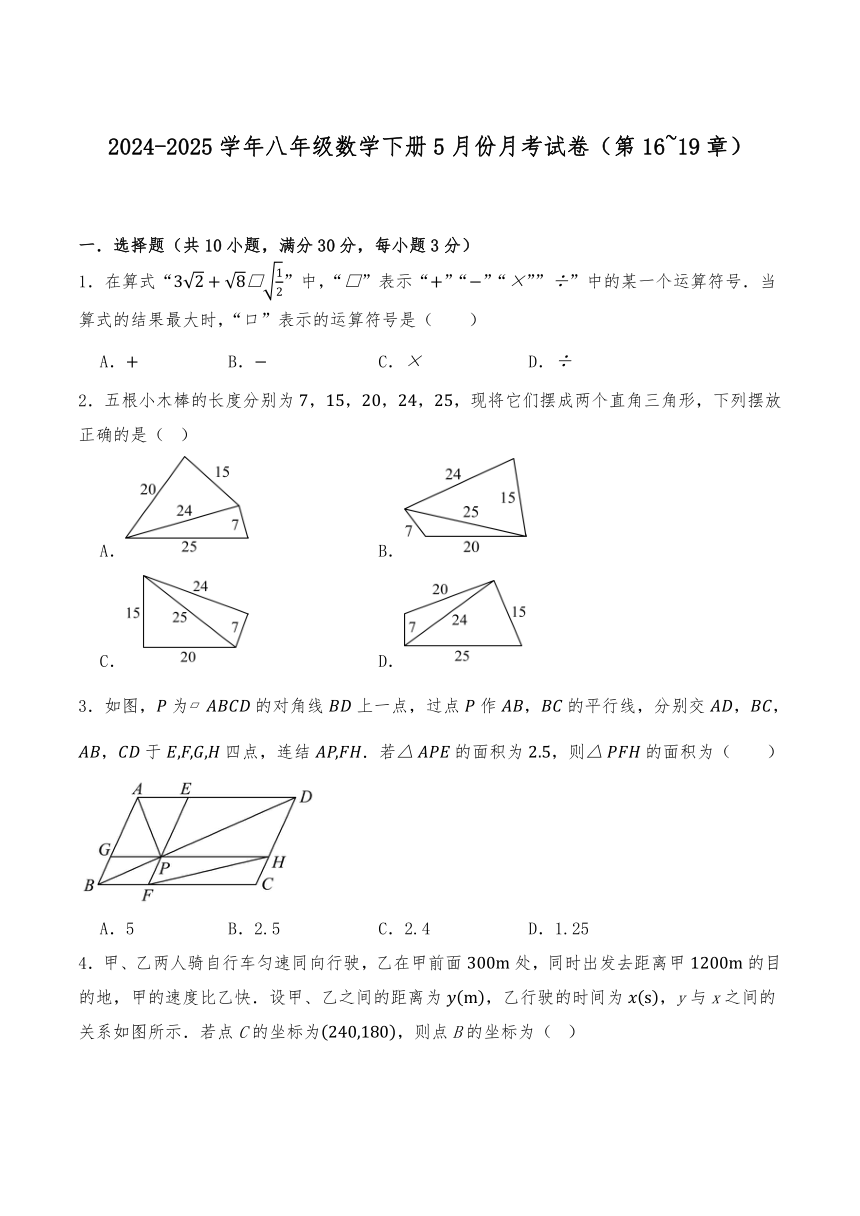
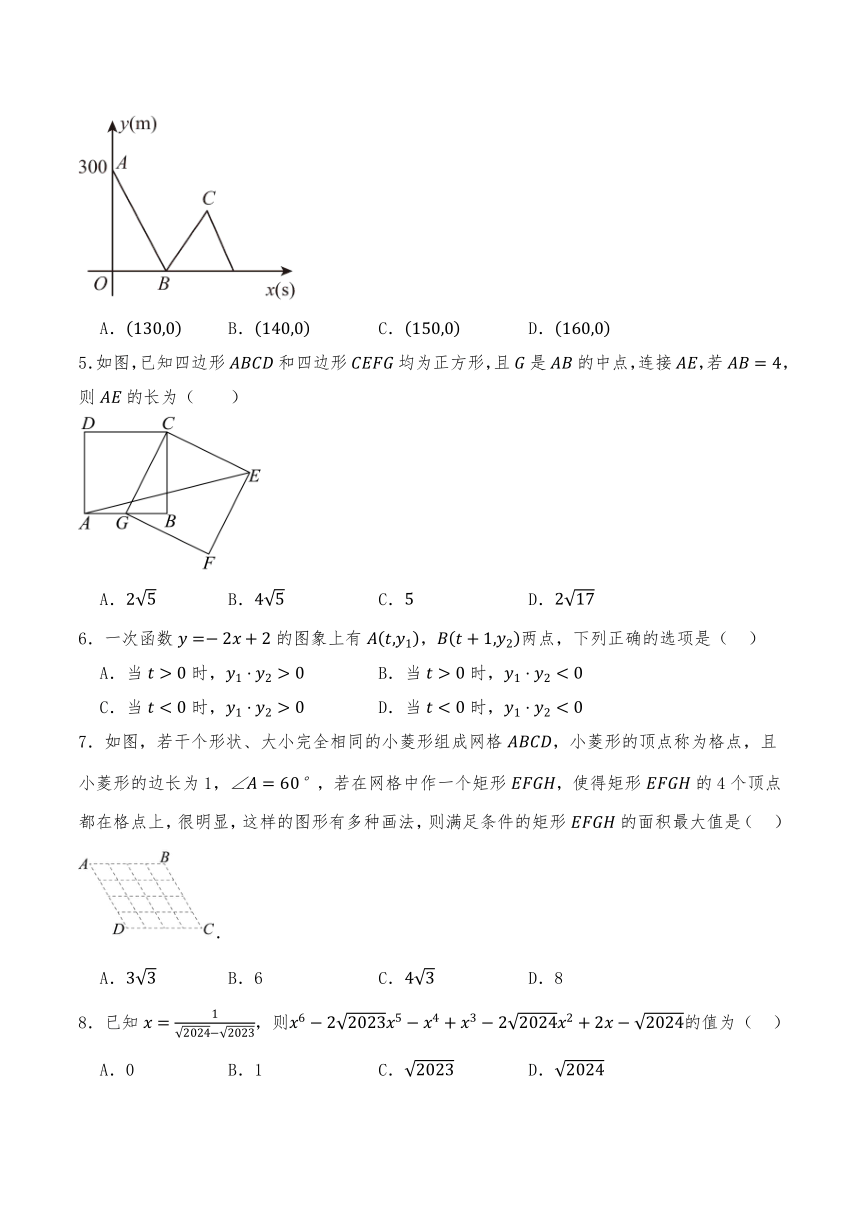
2024-2025学年八年级数学下册5月份月考试卷(第16~19章) 一.选择题(共10小题,满分30分,每小题3分) 1.在算式“”中,“”表示“”“”“”””中的某一个运算符号.当算式的结果最大时,“口”表示的运算符号是( ) A. B. C. D. 2.五根小木棒的长度分别为,,,,,现将它们摆成两个直角三角形,下列摆放正确的是( ) A. B. C. D. 3.如图,为的对角线上一点,过点作,的平行线,分别交,,,于四点,连结.若的面积为,则的面积为( ) A.5 B.2.5 C.2.4 D.1.25 4.甲、乙两人骑自行车匀速同向行驶,乙在甲前面处,同时出发去距离甲的目的地,甲的速度比乙快.设甲、乙之间的距离为,乙行驶的时间为,y与x之间的关系如图所示.若点C的坐标为,则点B的坐标为( ) A. B. C. D. 5.如图,已知四边形和四边形均为正方形,且是的中点,连接,若,则的长为( ) A. B. C. D. 6.一次函数的图象上有,两点,下列正确的选项是( ) A.当时, B.当时, C.当时, D.当时, 7.如图,若干个形状、大小完全相同的小菱形组成网格,小菱形的顶点称为格点,且小菱形的边长为1,,若在网格中作一个矩形,使得矩形的4个顶点都在格点上,很明显,这样的图形有多种画法,则满足条件的矩形的面积最大值是( ) . A. B.6 C. D.8 8.已知,则的值为( ) A.0 B.1 C. D. 9.如图,在中,,,点D为边上的中点,点E在线段上(点E不与点B,点D重合),过点A作交于点F,过点B作交的延长线于点G.若已知的长,则可求出( ) A.的长 B.的长 C.的长 D.的长 10.如图,在矩形中,,,P是的中点,点Q在边上,连接,将矩形沿折叠,点B,C,D的对应点分别为分别交于点E,F(点E在点F右侧),则线段的最大值为( ) A. B. C. D. 二.填空题(共6小题,满分18分,每小题3分) 11.如图,在直角三角形纸片中,,,.是中点,将纸片沿翻折,直角顶点的对应点为,交于,则 . 12.已知菱形,点分别为边的中点,若四边形的面积为,则菱形的面积为 . 13.青朱出入图(图1)是东汉末年数学家刘徽根据“割补术”运用数形关系证明勾股定理引入的图形,该图中的两个青入的三角形分别与两个青出的三角形全等,朱入与朱出的三角形全等,朱方与青方是两个正方形.为便于叙述,将其绘成图2,若记朱方对应正方形的边长为,青方对应正方形的边长为,已知,,则图2中的阴影部分面积为 . 14.【教材变式】已知为正整数,若是整数,则根据可知有最小值.设为正整数,若是大于1的整数,则的最小值与最大值的和是 . 15.如图,在平面直角坐标系中,点,,,…都在轴上,点,,,…都在同一条直线上,,,,,,…都是等腰直角三角形,且,则点的坐标是 . 16.如图,在矩形中,,E是边上的一动点,连接,过点D作交于点G,垂足为点F,连接. (1)当点G恰为中点时,则 . (2)当平分时,若,则 . 三.解答题(共8小题,满分72分) 17.(6分)先阅读下面的解答过程,再解决问题. 形如的化简,只要我们找到两个数,使,这样,于是; 举例:化简 解:这里 即, 用上述例题的方法化简: (1) (2) 18.(6分)如图,长方体的长,宽,高,三只蚂蚁沿长方体的表面同时以相同的速度从点出发到点处.蚂蚁甲的行走路径为翻过棱后到达点处(即),蚂蚁乙的行走路径为翻过棱后到达点处(即),蚂蚁丙的行走路径为翻过棱后到达点处(即). (1)甲、乙、丙三只蚂蚁的行走路程的最小值的平方分别是多少? (2)若三只蚂蚁都走自己的最短路径,请判断:哪只蚂蚁最先到达?哪只蚂蚁最后到达? 19.(8分)如图,在四边形中,,对角线交于点,过点作交的延长线于点,连接. (1)求证:; (2)若,求证:四边形是菱形; (3)在(2)的条件下, ... ...
~~ 已预览到文档结尾了 ~~