
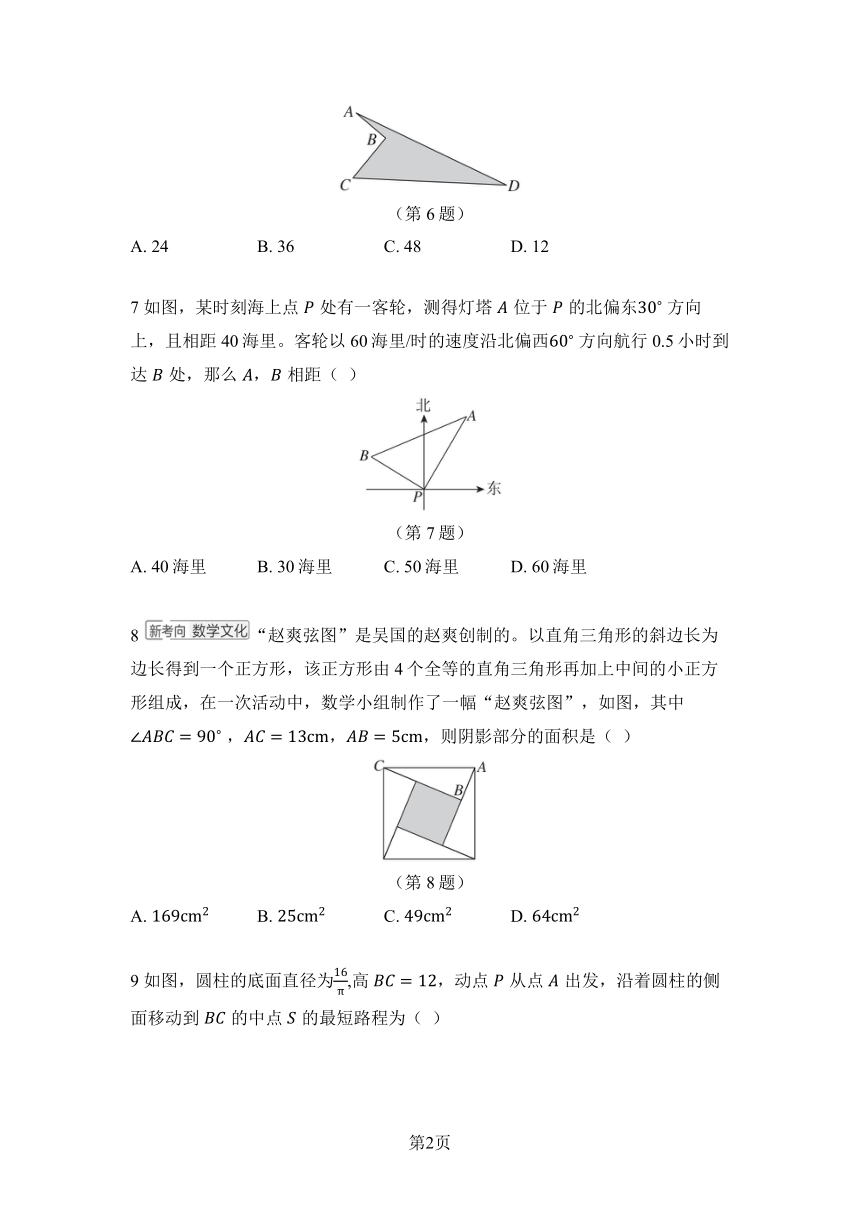
第一章 学情评估卷 一、选择题(每题3分,) 1 在中, ,,,的对边分别为,,。若,,则的值为( ) A. 13 B. 17 C. 7 D. 169 2 如图,在中, ,分别以的三边为边向外作三个正方形,其面积分别用,,表示。若,,则的值是( ) (第2题) A. 3 B. 5 C. 7 D. 9 3 如果将直角三角形的两直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的( ) A. 2倍 B. 3倍 C. 4倍 D. 以上都不对 4 直角三角形的两条直角边的长分别为6,8,则其斜边上的高为( ) A. 6 B. 8 C. 12 D. 5 满足下列条件时,不是直角三角形的为( ) A. ,, B. C. D. 6 如图,这是一块铁皮,测得,,,,,则铁皮的面积为( ) (第6题) A. 24 B. 36 C. 48 D. 12 7 如图,某时刻海上点处有一客轮,测得灯塔位于的北偏东 方向上,且相距40海里。客轮以60海里/时的速度沿北偏西 方向航行0.5小时到达处,那么,相距( ) (第7题) A. 40海里 B. 30海里 C. 50海里 D. 60海里 8 “赵爽弦图”是吴国的赵爽创制的。以直角三角形的斜边长为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次活动中,数学小组制作了一幅“赵爽弦图”,如图,其中 ,,,则阴影部分的面积是( ) (第8题) A. B. C. D. 9 如图,圆柱的底面直径为,高,动点从点出发,沿着圆柱的侧面移动到的中点的最短路程为( ) (第9题) A. 10 B. 12 C. 20 D. 14 10 如图,正方形的边长为4,点在边上,且,为对角线上一动点,连接,,则周长的最小值为( ) (第10题) A. 5 B. 6 C. 7 D. 8 二、填空题(每题3分,) 11 写出一组勾股数:_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 。 12 若等腰三角形中两个腰的长为,底边长为,则底边上的高为_ _ _ _ _ _ _ _ 。 13 已知,,是的三边长,且满足关系式,则的形状为_ _ _ _ _ _ _ _ _ _ _ _ _ _ 。 14 [[2025淮安月考]]如图,要为一段高为5米,长为13米的楼梯铺上红地毯,则红地毯的长至少为米。 (第14题) 15 [[2025成都期末]] 如图,一天傍晚,小方去小区遛狗,小方观察发现,她站直身体时,牵绳的手离地面的高度为分米,小狗的高分米,小狗与小方的手的水平距离分米(绳子一直是直的),则牵狗绳分米。 (第15题) 16 对角线互相垂直的四边形叫作“垂美”四边形,现有如图所示的“垂美”四边形,对角线,交于点。若,,则。 (第16题) 17 如图,在长方形中,,,点为上一点,将沿折叠,点恰好落在线段上的点处,则的长为_ _ _ _ 。 (第17题) 18 “勾股树”是以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边为边分别向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好似一棵树而得名。假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为_ _ 。 (第18题) 三、解答题() 19 (9分)在中,,,的对边分别为,,, 。 (1) 若,,求的值; (2) 若,,求的值; (3) 若,,求,的值。 20 (9分)如图所示,在每个小正方形的边长均为1的网格中,是格点图形(各顶点都在小正方形的顶点上),求中边上的高。 21 [[2025西安模拟]](10分) 如图,在中,,,。 (1) 判断的形状,并说明理由; (2) 若点为线段上一点,连接,且,求的面积。 22 (12分)定义:如图,点,把线段分割成,,,若以,,为边的三角形是一个直角三角形,则称点,是线段的勾股分割点。 (1) 已知点,把线段分割成,,,若,,,则点,是线段的勾股分割点吗?请说明理由。 (2) 已知点,是线段的勾股分割点,且为直角边,若,,求的长。 23 (12分)如图,一工厂位于点,河边原有两个取水点,,其中,由于某种原因从工厂到取水点的路受阻,为了取水更方便,工厂新建一个 ... ...
~~ 已预览到文档结尾了 ~~