沪科版七下(2024版)8.3.1 完全平方公式 学案

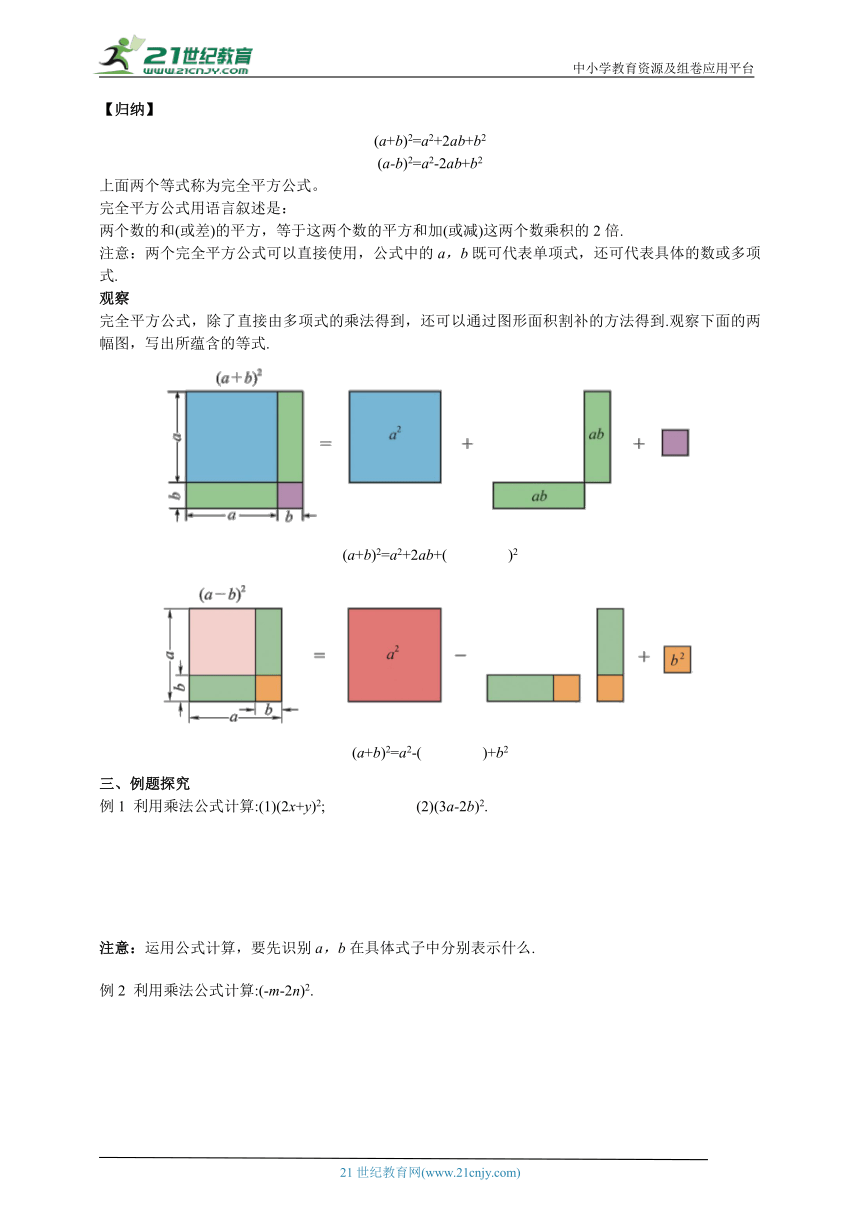
中小学教育资源及组卷应用平台 第8章 整式乘法与因式分解 8.3.1 完全平方公式 学习目标与重难点 学习目标： 1.会推导完全平方公式，理解公式的结构特征，并能正确利用公式进行乘法运算。 2.了解完全平方公式的几何背景。 3.经历探索完全平方公式的过程，进一步发展符号感和推理能力。 4.通过完全平方公式的发现和推导过程，培养观察、发现、归纳、概括、猜想等探究创新能力。 学习重点： 完全平方公式的推导及其应用及理解公式的结构特征和应用。 学习难点： 掌握完全平方公式的结构特征，理解公式中字母的广泛含义，能灵活运用公式进行简单的计算。 教学过程 一、问题导入 计算： (a+1)2=(a+1)(a+1)=_____=_____; (a+2)2=(a+2)(a+2)=_____=_____; (a+3)2=(a+3)(a+3)=_____=_____; (a-1)2=(a-1)(a-1)=_____=_____; (a-2)2=(a-2)(a-2)=_____=_____; (a-3)2=(a-3)(a-3)=_____=_____。 思考：观察上列等式，你有什么发现吗？ 二、新知探究 探究：完全平方公式 教材第74页 猜测：(a+b)2=_____; (a-b)2=_____。 验证：你能通过计算验证这两个等式吗？ 【归纳】 (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 上面两个等式称为完全平方公式。 完全平方公式用语言叙述是： 两个数的和(或差)的平方，等于这两个数的平方和加(或减)这两个数乘积的2倍. 注意：两个完全平方公式可以直接使用，公式中的a，b既可代表单项式，还可代表具体的数或多项式. 观察 完全平方公式，除了直接由多项式的乘法得到，还可以通过图形面积割补的方法得到.观察下面的两幅图，写出所蕴含的等式. (a+b)2=a2+2ab+( )2 (a+b)2=a2-( )+b2 三、例题探究 例1 利用乘法公式计算:(1)(2x+y)2;　　　　 (2)(3a-2b)2. 注意：运用公式计算，要先识别a，b在具体式子中分别表示什么. 例2 利用乘法公式计算:(-m-2n)2. 四、课堂练习 【知识技能类作业】 必做题 1.下列多项式中是完全平方式的有（ ） ① ② ③ ④ A．1个 B．2个 C．3个 D．4个 2.计算(2x+1)2的结果为 (　 ) A.-4x2+4x+1　　　 B.-4x2-4x-1　　　 C.4x2+4x+1　　　 D.4x2-4x-1 3.若，则的值为（ ） A．0 B．4 C．5 D．3或 选做题 4.若则的值为 ． 5.已知是完全平方式，则 ． 6.已知为实数，要使多项式是完全平方式，则k的值为 ． 【综合拓展类作业】 7.先化简，再求值：，其中． 五、课堂小结 这节课你收获了什么，在计算过程中须注意什么 六、作业布置 1.若为任意整数，则的值总能（ ） A．被整除 B．被整除 C．被整除 D．被整除 2.已知一个长方形的长为a，宽为b，它的面积为6，周长为12，则的值为（ ） A．16 B．28 C．24 D．22 3.下列图形阴影部分的面积能够直观地解释的是（ ） A． B． C． D． 4.已知，求下列各式的值； (1)； (2)； (3)． 答案解析 课堂练习： 1.【答案】B 【解析】解:依题意，是完全平方式，故①符合题意； 不是完全平方式，故②不符合题意； 不是完全平方式，故③不符合题意； 不是完全平方式，故④不符合题意； 故是完全平方式的只有① 2.【答案】C 【解析】解：(2x+1)2=4x2+4x+1　　　 3.【答案】D 【解析】解：∵， ∴， ∴， ∴，即，的值为或3． 4.【答案】 【解析】解：∵ ∴ ∴， ∴ 5.【答案】 【解析】解：是完全平方式， ， 即： 6.【答案】 【解析】解：∵ 7.【答案】解： . 当时，原式． 作业布置： 1.【答案】C 【解析】解： ， ∵为任意整数， ∴是整数， ∴的值总能被整除． 2.【答案】C 【解析】解：根据题意得：，， ∴， ∴． 3.【答案】D 【解析】解：A中，利用阴影部分的面积可得，故不符合题意； B中，利用阴影部分的面积可得，故不符合题意； C中，利用阴影部分的面积可得，故不符合题意； D中，利用阴影部分的面积可得，故符合题意． 4．【答案】(1)10 (2) (3) 【解析】解 ... ...