
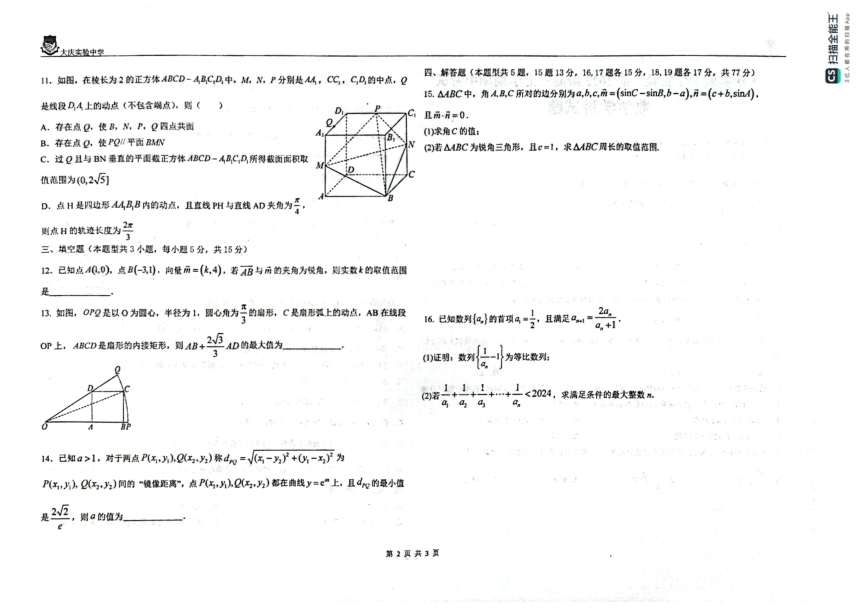
大庆实验中学实验二部 2022 级高三上学期期中考试 数学学科试题答案 选择题: 1 2 3 4 5 6 7 8 9 10 11 A C C A B B B B AD AD BCD 8.答案:B 取 DE 中点 F,三角形 ABC 的重心 G,则 A PA PB PC PD PE 3PG 3 2 2PF 5( PG PF ) 5 5 3 2 2 F 设 PH PG PF ,则可得GH HF ,设 BC 中点为 M,可得 D E 5 5 3 H P | MH | 12 3,CH 2 MH 2 CM 2 G 1332 B M C 所以 | PH |的最小值为 60 6 37 , | PA PB PC PD PE |的最小值为 300 30 37 11.答案:BCD 选项 A,连接 A1B,A1P,CD1 ,正方体中易知CD1 //A1B , P, N 分别是C1D1,C1C 中点,则 PN //CD1 ,所以 PN //A1B,即 A1,P,N ,B 四点共面,当Q与 A1重 合时满足 B,N,P,Q 四点共面,A 错误; 选项 B,如图,取 A1D1中点为Q,连接PQ,QM ,A1C1, 因为M ,N 分别是 AA1,CC1中点,则 A1M 与C1N 平行且相等, A1C1NM 是平行四边形, 所以MN //A1C1 ,又 P 是C1D1中点,所以PQ//A1C1,所以PQ//MN , MN 平面BMN ,PQ 平面BMN ,所以PQ// 平面BMN ,B 正确; D1 C1 选项 C,如图,在平面 A1B1C1D1上做QH B1C1于 H,过 H 做 HT BN 交 BC 或者CC Q H1 A1 B1 于 T,则BN 平面 QHT,如图,平面 QHT 截正方体 ABCD A1B1C1D1截面为平行四边形, N 当 T 与点 C 重合时,面积最大,此时, HT 5,QH 2,面积为 2 5 ,当 Q L T与点 D1 无限 D C 接近时,面积接近于 0 A A O B1 B1 选项 D,过点 P 做PO 平面 AA1B1B,交平面 AA1B1B于 O,则点 H 的轨迹为以 O 为圆 心,2 为半径的部分圆弧,设该圆弧与 AA1, B1B于 X,Y,如图,OX=OY=2,易得 X Y A B XOY 2 ,所以点 H 的轨迹长度为 3 3 填空题: 12.{k | k 1且k 16} 13. 2 3 3 14. a e Q '(y , x ax 1答案:设 2 2 )因为函数 y e 与 y ln x log xea 互为反函数, a y eax 1 与 y ln x 的图像关于直线 y x 对称, a 所以Q '(y2 , x ) 1 2 在 y ln x 上所以dPQ 的最小值为点 Р 到直线 y x 距离的最小值的两倍. a x0 e ax0 设 P( x0 , y0 ),则 PQ 2 2 eax0 x . min 2 0 设 f (x) 2 eax0 x 1 10 , f (x) 2aeax0 2 .由 f (x) 0得 x ln . a a x 1 1当 , ln 时, f (x) 0, f (x)a a 单调递减; x 1 1当 ln , 时, f (x) 0, f (x) 单调递增, a a f (x) 1 1 2 2 2 2 2所以 min f ln ln(ae),则| |的最小值是 ln a 1 .所以 a a ln a 1 , a a a e ln a 1 2 2 2 a,构造函数 h(a) ln a 1 a , h(e) ln e 1 e 0求导后解得 a e e e e 解答题: 15.在VABC 中,角 A, B,C 所对的边分别为 a,b,c,m sinC sinB,b a ,n c b,sinA ,且m n 0 . (1)求角C 的值; (2)若VABC 为锐角三角形,且 c 1,求 ABC 周长的取值范围. m 答案:(1) n 0 所以 sinA a b sinB sinC b c 0 利用正弦定理化简得: a a b b c b c 0即 a2 b2 c2 ab, 2 2 2 由余弦定理可得 cosC a b c 1 , 2ab 2 又因为C 0, π π,所以C ; 3 2π (2)由(1)得 A B ,即B 2π A, 3 3 又因为三角形 ABC 为锐角三角形, 0 2π A π 3 2 π π 所以 解之得: A , 6 20 A π 2 a b c 1 2 因为 c 1,由正弦定理得: sinA sinB sinC sin π 3 , 3 2 所以 a sinA,b 2 sinB, 3 3 a b 2 sinA 2 sinB 2 sinA 2 sin π A 2sin A π所以 3 3 3 3 3 6 π π π 2π 因为 A π ,所以 A , 6 2 3 6 3 所以 3 2sin A π 2 a b 3,2 . 1 3,3 6 ,则 的取值范围为 , ABC 周长的取值范围 2a 16. 已知数列 an 1 n 的首项 a1 ,且满足 an 1 a 1. 2 n 1 (1)证明:数列 1 为等比数列; an 1 1 1 1(2)若 2024a a a a ,求满足条件的最大整数 n. 1 2 3 n a 2a1 n 1 an 1 1 1 1 答案::( )由 n 1 得 a 1 a , n n 1 2an 2 an 2 1 1 则 1 1 1 1 , 1 1 0 an 1 2 an a1 1 1 1 所以数列 1 是首项为 1 1,公比为 的等比 ... ...
~~ 已预览到文档结尾了 ~~