确定圆的条件(学案带答案)

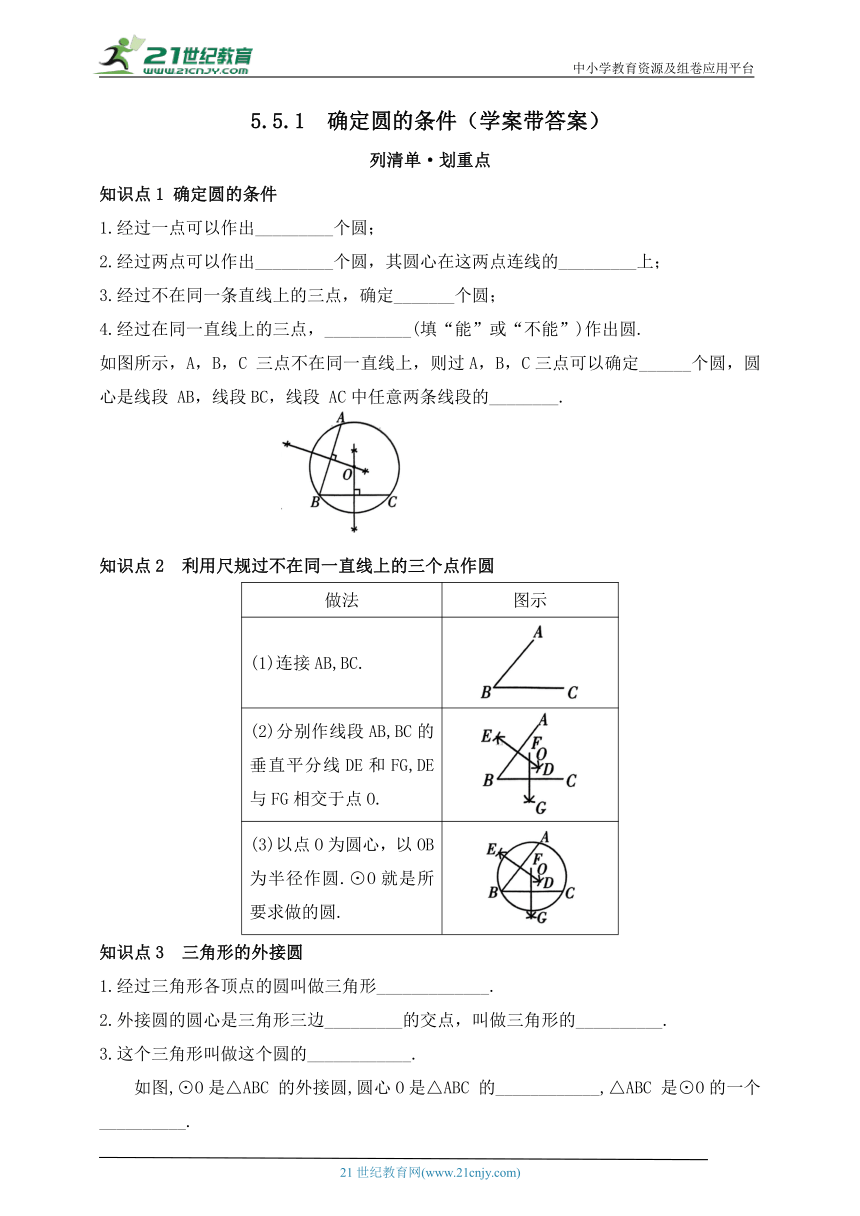
中小学教育资源及组卷应用平台 5.5.1 确定圆的条件（学案带答案） 列清单·划重点 知识点1 确定圆的条件 1.经过一点可以作出_____个圆； 2.经过两点可以作出_____个圆，其圆心在这两点连线的_____上； 3.经过不在同一条直线上的三点，确定_____个圆； 4.经过在同一直线上的三点，_____(填“能”或“不能”)作出圆. 如图所示，A，B，C 三点不在同一直线上，则过A，B，C三点可以确定_____个圆，圆心是线段 AB，线段BC，线段 AC中任意两条线段的_____. 知识点2 利用尺规过不在同一直线上的三个点作圆 做法 图示 (1)连接AB,BC. (2)分别作线段AB,BC的垂直平分线DE和FG,DE与FG相交于点O. (3)以点O为圆心，以OB为半径作圆.⊙O就是所要求做的圆. 知识点3 三角形的外接圆 1.经过三角形各顶点的圆叫做三角形_____. 2.外接圆的圆心是三角形三边_____的交点，叫做三角形的_____. 3.这个三角形叫做这个圆的_____. 如图,⊙O是△ABC 的外接圆,圆心O是△ABC 的_____,△ABC 是⊙O的一个_____. 注意 (1)锐角三角形的外心在三角形内；直角三角形的外心为斜边中点；钝角三角形的外心在三角形外. (2)任意三角形有且只有一个外接圆；任意一个圆可以有无数个内接三角形. (3)三角形的外心到三角形各顶点的距离相等. (4)直角三角形的外心是斜边的中点，外接圆的直径即为斜边边长. 明考点·识方法 考点1 确定圆的条件 典例1 小明不慎把家里的圆形玻璃打碎了，带如图所示的玻璃碎片到商店配与原来大小一样的圆形玻璃，以下是工作人员排乱的操作步骤： ①连接AB 和BC ②在玻璃碎片上任意找不在同一直线上的三点 A,B,C ③以点O 为圆心，OA 为半径作⊙O ④分别作出AB 和BC 的垂直平分线，并且相交于点O 正确的操作步骤是 ( ) A.②①③④ B.②①④③ C.①②④③ D.①④②③ 思路导析 本题考查了确定圆的条件：经过不在同一条直线上的三点，确定一个圆.这块玻璃碎片的圆心是线段AB 和线段BC 垂直平分线的交点，∴正确的操作步骤是②①④③. 变式 如图,点 A,B,C,D均在直线上，点P 在直线l 外，则经过其中任意三个点，最多可画出圆的个数为 ( ) A. 3个 B. 4个 C. 5个 D. 6个 考点2 三角形的外接圆 典例2 如图，⊙O是等边△ABC 的外接圆,若 AB=3,则⊙O的半径是 ( ) A. C. D. 思路导析 作直径AD，连接CD，利用等边三角形的性质得到 由圆周角定理的推论得到∠ACD=90°,∠D=∠B=60°,然后利用特殊角的三角函数值求解. 变式 如图,△ABC 是⊙O的内接三角形,若OA∥CB,∠ACB=25°,则∠CAB=_____. 当堂测·夯基础 1.如图,△ABC 内接于⊙O,若 则∠A等于 ( ) A. 67° B. 62° C. 57° D. 72° 2.如图, 内接于⊙O，CD 是⊙O 的直径,连接 BD, 则 的度数是 ( ) A. 41° B. 45° C. 49° 3.如图，在平面直角坐标系 xOy中,点 A,B,C的横、纵坐标都为整数，过这三个点作一条圆弧，则此圆的圆心坐标是_____. 4.如图,⊙O是 的外接圆,连接 OA 交 BC于点 D. (1)求证: 与 互余； (2)若 求⊙O的半径. 5.如图1, 内接于⊙O,D 为 BC 上一点,连接 AD,AO, (1)如图1,求证: (2)如图2,延长AD交⊙O于点 H,连接CH,若 求⊙O的半径. 6.如图, 是⊙O的内接三角形，AB 为⊙O 的直径，CD 平分∠ACB,交⊙O 于点 D,连接AD,点 E在弦CD 上,且 连接AE. (1)求证: (2)若 求AE的长. 参考答案 【列清单·划重点】 知识点 1 1.无数 2.无数 垂直平分线 3. 1 4. 不能 1 垂直平分线的交点 知识点3 1.外接圆 2.垂直平分线 外心 3.内接三角形 外心 内接三角形 【明考点·识方法】 典例1 B 变式 D 典例 2 C 解析：作直径AD,连接CD,如图所示. 为等边三角形， ∵AD为⊙O的直径, 变式 【当堂测·夯基础】 1. A 2. C 3.(2,1) 4.解:(1)证明:延长 AD 交圆O于点 E,连接CE, ∵AE是直径, 即 与 互余； (2)∵∠B=∠E,∠ADB=∠CDE,∴△ ... ...