
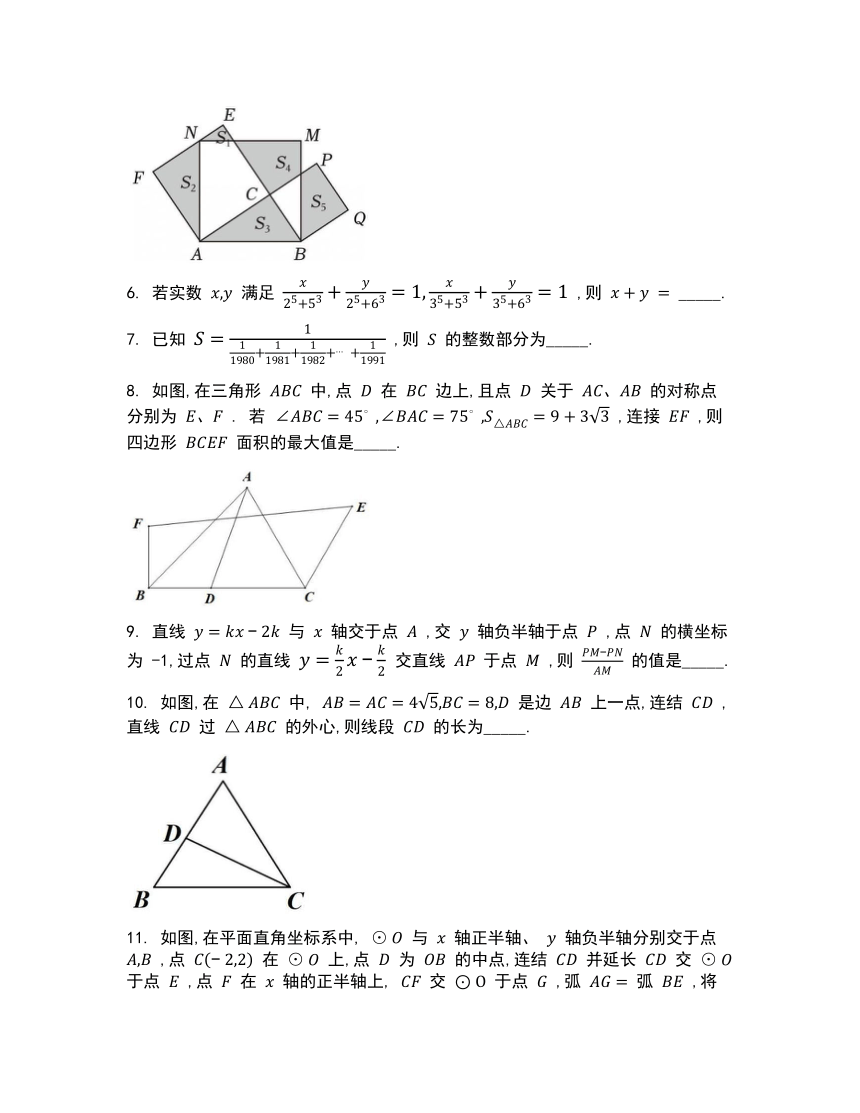
25.05 鄞州实验初三培优加试考数学试卷 一、填空题 1. 设 是一个四位数, 是阿拉伯数字,且 , 则式子 的最大值是_____. 2. 将号码分别为 的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球,号码为 ,放回后乙再摸出一个球,号码为 ,则使不等式 成立的事件发生的概率为_____. 3. [x]表示不超过 的最大整数,如 [3.2] ,已知正整数 小于 2025, 且 ,则这样的 有_____个. 4. 已知 中, 是边 的中点, 延长线上的点 满足 的内切圆与边 的切点分别为 ,连结 分别与 的延长线交于 ,则 的值为_____. 5. 如图,以 为斜边的直角三角形 的每条边为边作正方形 , 正方形 ,正方形 ,且边 恰好经过点 .若 ,则阴影部分的面积为_____(用含 的代数式表示). 6. 若实数 满足 ,则 _____. 7. 已知 ,则 的整数部分为_____. 8. 如图,在三角形 中,点 在 边上,且点 关于 的对称点分别为 . 若 ,连接 ,则四边形 面积的最大值是_____. 9. 直线 与 轴交于点 ,交 轴负半轴于点 ,点 的横坐标为 -1,过点 的直线 交直线 于点 ,则 的值是_____. 10. 如图,在 中, 是边 上一点,连结 ,直线 过 的外心,则线段 的长为_____. 11. 如图,在平面直角坐标系中, 与 轴正半轴、 轴负半轴分别交于点 ,点 在 上,点 为 的中点,连结 并延长 交 于点 ,点 在 轴的正半轴上, 交 于点 ,弧 弧 ,将点 向右平移 个单位,点 向上平移 个单位后,两点均在函数 的图象上,则 关于 的函数关系式_____. 12. 设正整数 ,满足 ,且 ,则 的值是_____. 二、简答题 13. 已知二次函数 ,当 时,恒有 ,且关于 的方程 的两个实数根的倒数和小于 . 求 的取值范围. 14. 如图,圆内接六边形 满足 ,且对角线 , 相交于一点 ,设 与 的交点为 . 求证:(1) . 25.05 鄞州实验初三培优加试考数学试卷全解全析 1.【解析】 原式 , 当 时,原式最大值 . 2. ,则 枚举: 时, ; 时, ; 时, ; 时, ; 时, ; 此事件的概率是 . 3.【解析】 (当且仅当 ,取到 “ ” ) 当 时,则 为整数, 为 6 的倍数, 余 2, 有337个. 4.【解析】连结 ,设 , , 由 为 中点, , 又 , 由 ①, 由 为 的内切圆圆心, 分别为边 上的切点, 四边形 为正方形, , ②, 综合①②得 . 5.【解析】过 作 垂直 ,连结 , 由题意易证 、 、 , 故 , , , , , ,故 三点共线, 从而易证 , 设 ,则 ,由勾股定理 , 即 . 6. 【解析】注意到上面三个方程中分母 2、3 在变化,我们用 代替这些数字的位置,得到方程 ,去分母得 , 若将其看成关于 的方程,则这是一个一元二次方程,且其解为 , 因此我们将其展开: , 由韦达定理可知 ,即 . 7.【解析】分母是从 1980 到 1991 的倒数之和, 共 1991-1980+1=12 项. 每一项 ,分子越大,分数越小, 的分母中的项递减,因此 , 化为假分数得 ,故 的整数部分为 165. 8.【解析】如图,连结 ,作 交 的延长线于 于 . 为等腰直角三角形, , 设 , ,解得: . 由翻折的性质可知: , 五边形 的面积 ,为定值, 又 , 的面积最小时,四边形 的面积最大, , 的值最小时,即当 的值最小时, 的面积最小,此时 与 重合,最小值 , 四边形 的面积最大值 . 9.【解析】由题意可知 , 联立 ,得 , ,同理可知 , , . 10.【解析】作三角形 的外接圆圆 ,作 于点 ,连结 并延长交 于点 ,则 , , 在 中, ,即 , 设 ,则 . 11. 【解析】由题意可知 , 连结 , 弧 弧 , , 易知 , , , , , 由题意可知: . 12.【解析】 , 又 可设 ,所以 . 13.【解析】由 时,恒有 , 即 , 当 时, ,当 时, ,解得 , 设 的两个实数根为 , 由韦达定理可知 , 从而 ,解得 或 , 综上 . 14.【解析】(1) ,即 , ,又 , , ,即 ; (2) , ,即 , 又 . ... ...
~~ 已预览到文档结尾了 ~~