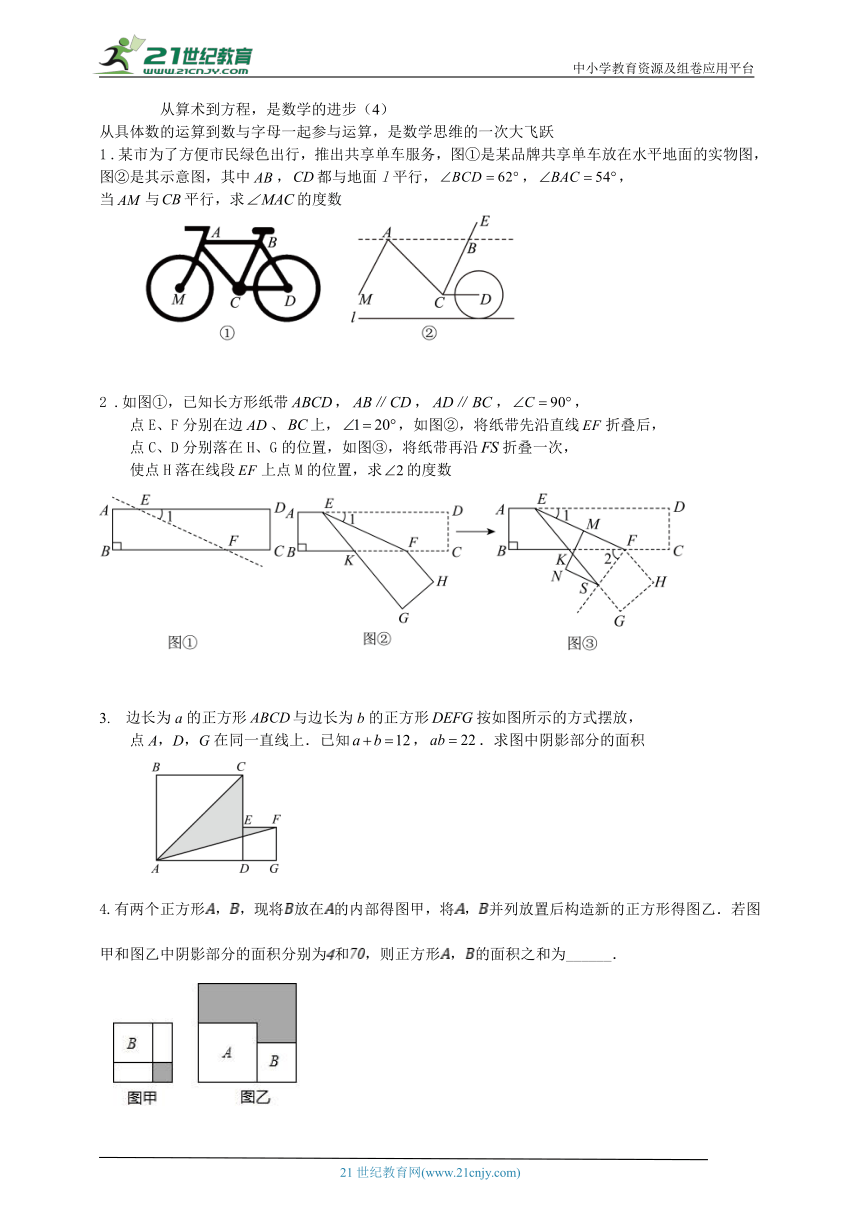

中小学教育资源及组卷应用平台 从算术到方程,是数学的进步(4) 从具体数的运算到数与字母一起参与运算,是数学思维的一次大飞跃 1 .某市为了方便市民绿色出行,推出共享单车服务,图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中,都与地面l平行,,, 当与平行,求的度数 2 .如图①,已知长方形纸带,,,, 点E、F分别在边、上,,如图②,将纸带先沿直线折叠后, 点C、D分别落在H、G的位置,如图③,将纸带再沿折叠一次, 使点H落在线段上点M的位置,求的度数 3. 边长为a的正方形与边长为b的正方形按如图所示的方式摆放, 点A,D,G在同一直线上.已知,.求图中阴影部分的面积 4.有两个正方形,,现将放在的内部得图甲,将,并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为和,则正方形,的面积之和为_____. 5..小磊和小轩在课外练习中碰到了一个问题,需要对多项式 进行因式分解. 小磊认为该整式一定有一个因式 ,小轩认为必有因式是 ,两人找到老师寻求帮助. 老师提供了一个方法: 因式分解是整式乘法的逆运算. 若整式 能被整式 整除,则 必为 的一个因式. 老师给出了演算方法: (1)观察老师的演算后,你认为__ _ (2)已知多项式 的其中一个因式为 ,请试着根据老师的方法列出演算过程, 6.为了迎接在杭州举行的第19届亚运会,某旅游商店购进若干吉祥物钥匙扣和明信片,已知吉祥物钥匙扣的进价为20元/个,明信片的进价为5元/套.一个吉祥物钥匙扣的售价比一套明信片的售价高20元.若顾客花180元购买的吉祥物钥匙扣数量与花60元购买的明信片数量相同. (1)求吉祥物钥匙扣和明信片的售价. (2)为了促销,商店对吉祥物钥匙扣进行9折销售.某顾客同时购买吉祥物钥匙扣和明信片两种商品若干件,商家获毛利润100元,请问有几种购买方案. 7.用不同的方法计算图中阴影部分的面积,得到等式:_____ _;图是由两个边长分别为、、的直角三角形和一个两条直角边都是的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由; 在直角中,,三边分别为、、,,,求的值; 8.用几个小的长方形、正方形拼成一个大的正方形,然后利用两种不同的方法计算这个大的正方形的面积,可以得到一个等式,例如:计算图1的面积.把图1看作一个大正方形. 它的面积是;如果把图1 看作是由2个长方形和2个小正方形组成的,它的面积为,由此得到. (1)如图2,由几个面积不等的小正方形和几个小长方形拼成一个边长为的正方形,从中你能发现什么结论?该结论用等式表示为 . (2)利用(1)中的结论解决以下问题: 已知,,求的值; (3)如图3,正方形边长为a,正方形边长为b,点D,G,C在同一直线上,连接、,若,,求图3中阴影部分的面积. 9.如图所示的长方形中,甲、乙、丙、丁四个区域的面积相等,若甲区域的长是宽的2倍,求乙区域的长与宽的比 10.有红、黄、绿三块大小一样的正方形纸片,放在一个底面积为128cm2的正方形盒内,它们之间互相叠合,如图所示,已知露在外的部分中,红色、黄色和绿色三块面积之比为10:7:5.记没被盖住的两部分的面积分别为a cm2和b cm2 求a+b的值 1.解:∵,都与地面l平行,∴,∴, ∴, ∵,,∴,∴当时,. 2.解:由折叠可得:, ,.,∴,∴, ,,, 3.解:由图可知:, 正方形边长为a,正方形边长为b, , 将,代入得:, 4.【详解】解:设正方形A的边长为a,正方形B的边长为b, 由图甲得,, 由图乙得,,所以, 5.小磊正确2.(x-3)(x2-3x-2) 6.(1)设吉祥物钥匙扣的售价为x元,则明信片的售价为元, 由题意得:,解得:, 经检验,是原方程的解,且符合题意,则; 答:吉祥物钥匙扣的售价为30元,明信片的售价为10元. (2)设购买吉祥物钥匙扣m ... ...
~~ 已预览到文档结尾了 ~~