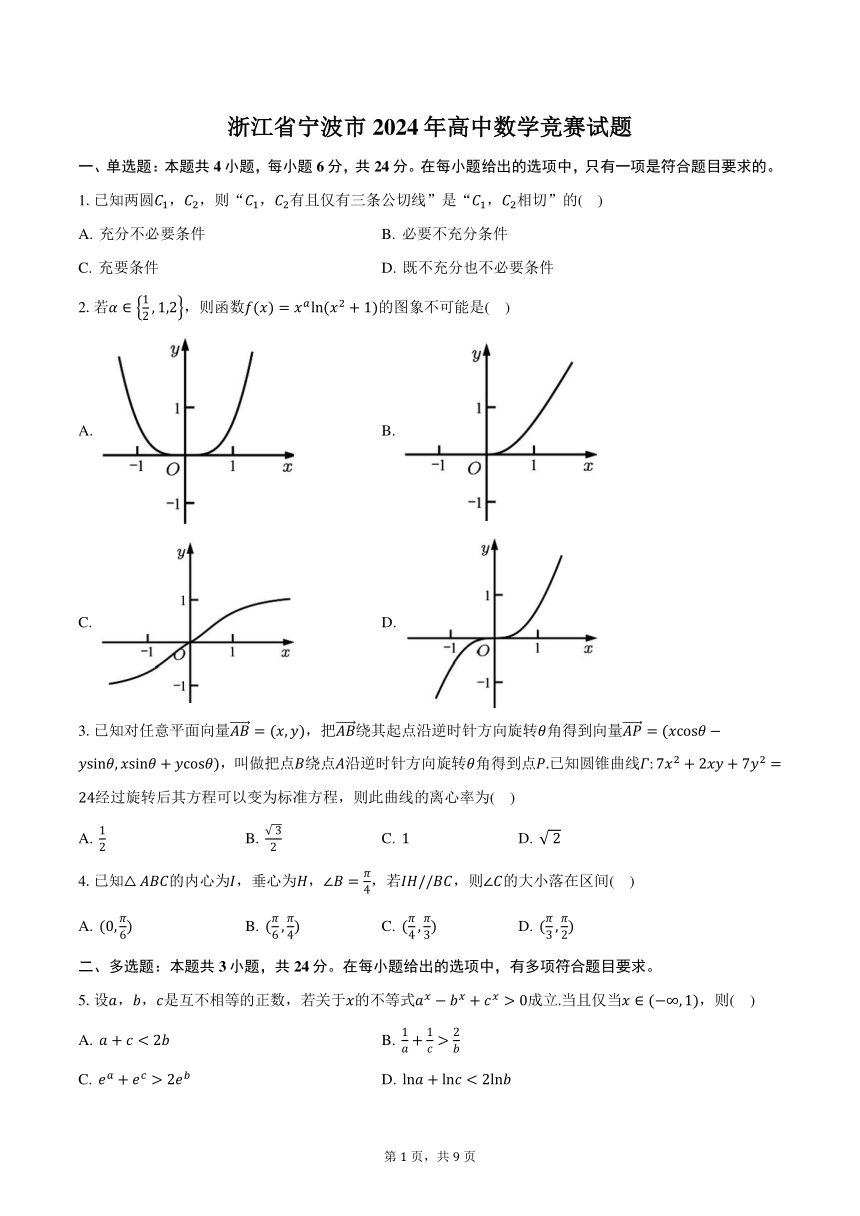

浙江省宁波市 2024 年高中数学竞赛试题 一、单选题:本题共 4 小题,每小题 6 分,共 24 分。在每小题给出的选项中,只有一项是符合题目要求的。 1.已知两圆 1, 2,则“ 1, 2有且仅有三条公切线”是“ 1, 2相切”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 1 2.若 ∈ { , 1,2},则函数 ( ) = ln( 2 + 1)的图象不可能是( ) 2 A. B. C. D. 3.已知对任意平面向量 = ( , ),把 绕其起点沿逆时针方向旋转 角得到向量 = ( cos sin , sin + cos ),叫做把点 绕点 沿逆时针方向旋转 角得到点 .已知圆锥曲线 : 7 2 + 2 + 7 2 = 24经过旋转后其方程可以变为标准方程,则此曲线的离心率为( ) 1 √ 3 A. B. C. 1 D. √ 2 2 2 4.已知△ 的内心为 ,垂心为 ,∠ = ,若 // ,则∠ 的大小落在区间( ) 4 A. (0, ) B. ( , ) C. ( , ) D. ( , ) 6 6 4 4 3 3 2 二、多选题:本题共 3 小题,共 24 分。在每小题给出的选项中,有多项符合题目要求。 5.设 , , 是互不相等的正数,若关于 的不等式 + > 0成立.当且仅当 ∈ ( ∞,1),则( ) 1 1 2 A. + < 2 B. + > C. + > 2 D. ln + ln < 2ln 第 1 页,共 9 页 6.数列{ }是等差数列,周期数列{ }满足 = cos( ).若集合 = { | = , ∈ },中恰有三个元素, 则数列{ }的周期 的取值可能是( ) A. 4 B. 5 C. 6 D. 7 7.已知棱长为2的正方体 1 1 1 1,点 是线段 1 1上的动点,点 在侧面 1 1(包含边界)上且 满足 1 1 = 0,下列结论正确的是( ) A. 对任意的点 ,总存在点 使得 ⊥ B. 三棱锥 外接球的球心可以是线段 的中点 9√ 2 C. 三棱锥 外接球半径的最小值为 8 7√ 2 D. 二面角 的正切的最大值为 2 三、填空题:本题共 6 小题,每小题 8 分,共 48 分。 1 8.已知函数 ( ),满足 ( ) + ( ) = ,则 (2) = . 1 9.在斜三棱柱的9条棱中任取2条,则取出的两条棱所在直线异面的概率为 . 10.在3 × 3的方格表内填入1,2, ,9,若任何有公共边的两格内填的数之差的绝对值都不小于 ,则 的 最大值为 . 11.已知9位学生在某次数学测试中的成绩的平均值为75,方差为80,则这9位学生成绩的中位数的最大值 为 . 12.设 ( 0, 0)为椭圆 2 + 4 2 = 2 2与直线 + 2 = 2 + 2的交点,则过 ( 0, 0), (2,1)分别作两 坐标轴的垂线围成的矩形的面积的最大值为 . 1 √ 3 13.已知复数 1, 2满足| 1 | = √ 2,且 2 = + ,则| ( 1)| + | ( 2)|的取值范围为 . (注: ( ) 1 2 2 表示 的实部) 四、解答题:本题共 5 小题,共 104 分。解答应写出文字说明,证明过程或演算步骤。 14.(本小题17分) 在△ 中,角 , , 所对边分别为 , , ,且 2 + 2 sin2 = 2cosA. 2 (1)判断△ 的形状,并说明理由; (2)若△ 为等腰三角形, 为边 上一动点,作 ⊥ 于 点,求 的最小值. 15.(本小题17分) 1 已知函数 ( ) = . √ 第 2 页,共 9 页 ( )+ ( +2) (1)求证: > ( + 1); 2 (2)若关于 的不等式1 ≤ ( + 1) ≤ 1 的解集为[0,3],求实数 和 的取值范围. 16.(本小题20分) 已知双曲线 : 2 2 = 2的左、右焦点分别为 1, 2,过点 1的直线分别交双曲线 的两支于 , 两点, 直线 2 , 2 与直线 = 1分别交于点 , . (1)若 为线段 上一点,满足 △ 2 = △ .求点 的轨迹方程; 2 1(2)若 = , 1 = ,求 4 4 △ 2 的取值范围. 17.(本小题25分) 1 已知 为素数,定义 ( )表示正整数 的不被 整除的最大因子.记 = ∑ =1 ( ). 2 2 求证:(1){ +1 }为等比数列; (2)∑ =1 < . ( 1)2 18.(本小题25分) 设集合 = { 1, 2, , }, ∈ , = 1,2, , .将 的每个子集的元素相加,得到2 个数(空集的元素 记为0),将这些数按照不减的顺序排列,得到一组数 1, 2, , 2 . (1)若 = {1,2,4, , 2 1},证明:若 ≠ ,则 ≠ ; (2)若 1, ... ...
~~ 已预览到文档结尾了 ~~