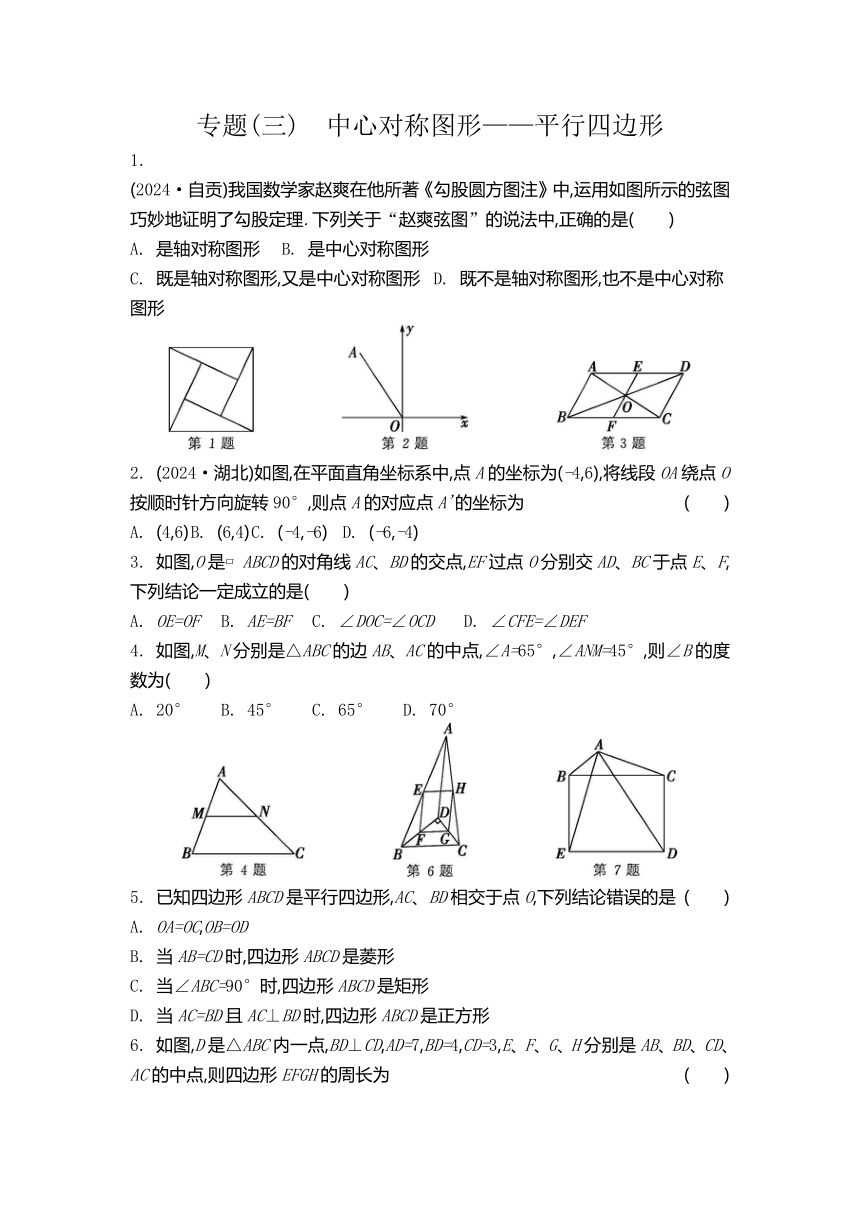
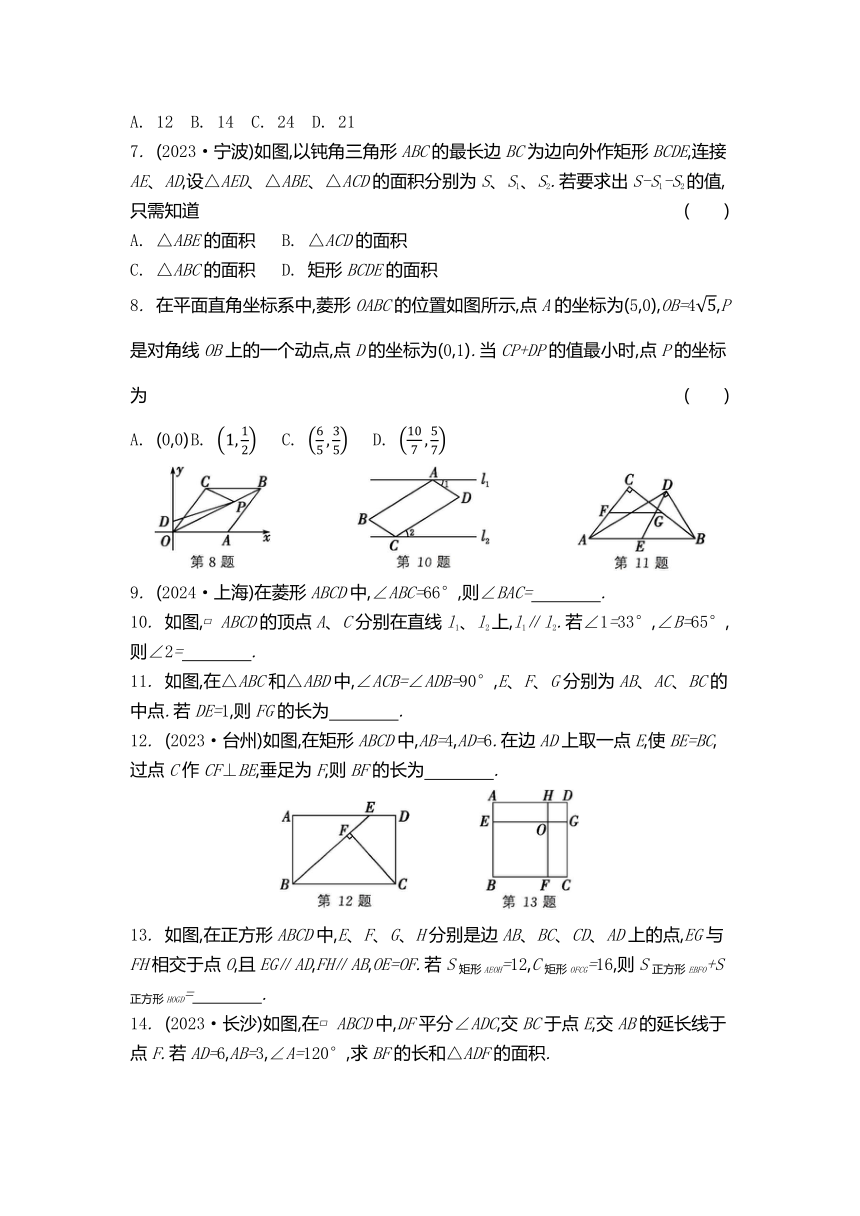
专题(三) 中心对称图形———平行四边形 1. (2024·自贡)我国数学家赵爽在他所著《勾股圆方图注》中,运用如图所示的弦图巧妙地证明了勾股定理.下列关于“赵爽弦图”的说法中,正确的是( ) A. 是轴对称图形 B. 是中心对称图形 C. 既是轴对称图形,又是中心对称图形 D. 既不是轴对称图形,也不是中心对称图形 2. (2024·湖北)如图,在平面直角坐标系中,点A的坐标为(-4,6),将线段OA绕点O按顺时针方向旋转90°,则点A的对应点A'的坐标为 ( ) A. (4,6) B. (6,4) C. (-4,-6) D. (-6,-4) 3. 如图,O是 ABCD的对角线AC、BD的交点,EF过点O分别交AD、BC于点E、F,下列结论一定成立的是( ) A. OE=OF B. AE=BF C. ∠DOC=∠OCD D. ∠CFE=∠DEF 4. 如图,M、N分别是△ABC的边AB、AC的中点,∠A=65°,∠ANM=45°,则∠B的度数为( ) A. 20° B. 45° C. 65° D. 70° 5. 已知四边形ABCD是平行四边形,AC、BD相交于点O,下列结论错误的是 ( ) A. OA=OC,OB=OD B. 当AB=CD时,四边形ABCD是菱形 C. 当∠ABC=90°时,四边形ABCD是矩形 D. 当AC=BD且AC⊥BD时,四边形ABCD是正方形 6. 如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E、F、G、H分别是AB、BD、CD、AC的中点,则四边形EFGH的周长为 ( ) A. 12 B. 14 C. 24 D. 21 7. (2023·宁波)如图,以钝角三角形ABC的最长边BC为边向外作矩形BCDE,连接AE、AD,设△AED、△ABE、△ACD的面积分别为S、S1、S2.若要求出S-S1-S2的值,只需知道 ( ) A. △ABE的面积 B. △ACD的面积 C. △ABC的面积 D. 矩形BCDE的面积 8. 在平面直角坐标系中,菱形OABC的位置如图所示,点A的坐标为(5,0),OB=4,P是对角线OB上的一个动点,点D的坐标为(0,1).当CP+DP的值最小时,点P的坐标为 ( ) A. (0,0) B. C. D. 9. (2024·上海)在菱形ABCD中,∠ABC=66°,则∠BAC= . 10. 如图, ABCD的顶点A、C分别在直线l1、l2上,l1∥l2.若∠1=33°,∠B=65°,则∠2= . 11. 如图,在△ABC和△ABD中,∠ACB=∠ADB=90°,E、F、G分别为AB、AC、BC的中点.若DE=1,则FG的长为 . 12. (2023·台州)如图,在矩形ABCD中,AB=4,AD=6.在边AD上取一点E,使BE=BC,过点C作CF⊥BE,垂足为F,则BF的长为 . 13. 如图,在正方形ABCD中,E、F、G、H分别是边AB、BC、CD、AD上的点,EG与FH相交于点O,且EG∥AD,FH∥AB,OE=OF.若S矩形AEOH=12,C矩形OFCG=16,则S正方形EBFO+S正方形HOGD= . 14. (2023·长沙)如图,在 ABCD中,DF平分∠ADC,交BC于点E,交AB的延长线于点F.若AD=6,AB=3,∠A=120°,求BF的长和△ADF的面积. 第14题 15. 如图,在四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC. (1) 求证:四边形ABCD是菱形; (2) 如果BE=BC,且∠CBE∶∠BCE=2∶3,求证:四边形ABCD是正方形. 第15题 16. 如图,△ABC是锐角三角形,分别以AB、AC为边向外作等边三角形ABM和等边三角形CAN,D、E、F分别是MB、BC、CN的中点,连接DE、FE,求证:DE=EF. 第16题 17. 如图,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,CD=4,∠C=45°,P是边BC上的一个动点,设PB的长为x. (1) 当x的值为 时,以P、A、D、E为顶点的四边形是平行四边形. (2) 在点P运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形 请说明理由. 第17题 18. 将矩形ABCD绕点A按顺时针方向旋转α(0°<α<360°),得到矩形AEFG. (1) 如图,当点E在BD上时,连接DF.求证:FD=CD. (2) 连接GC、GB,当α为多少时,GC=GB 请说明理由,并画出图形. 第18题 19. 如图①,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H. (1) 如图②,将△ADF绕点A按顺时针方向旋转90°得到△ABG,求证:△AGE≌△AFE ... ...
~~ 已预览到文档结尾了 ~~