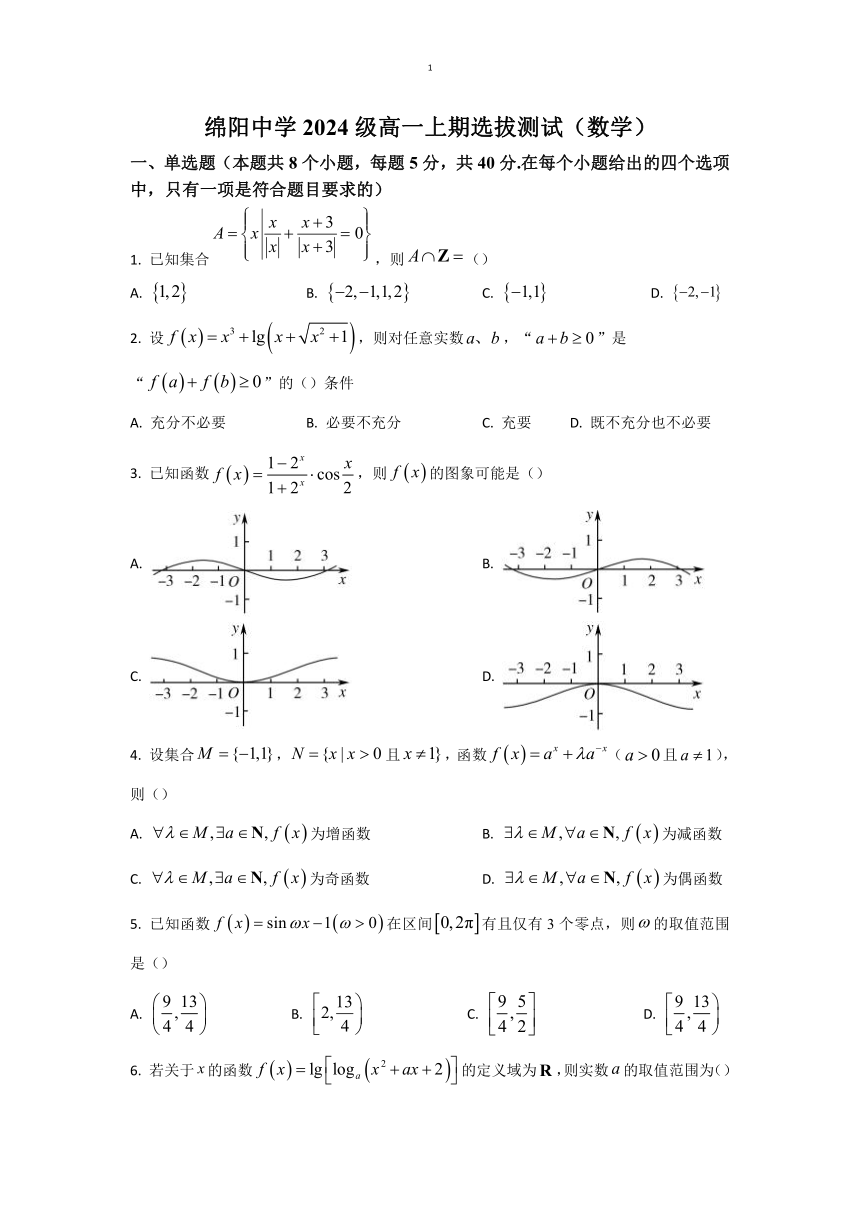

1 绵阳中学2024级高一上期选拔测试(数学) 一、单选题(本题共8个小题,每题5分,.在每个小题给出的四个选项中,只有一项是符合题目要求的) 1. 已知集合,则() A. B. C. D. 2. 设,则对任意实数,“”是“”的()条件 A. 充分不必要 B. 必要不充分 C. 充要 D. 既不充分也不必要 3. 已知函数,则的图象可能是() A. B. C. D. 4. 设集合,且,函数(且),则() A. 为增函数 B. 为减函数 C. 为奇函数 D. 为偶函数 5. 已知函数在区间有且仅有3个零点,则的取值范围是() A. B. C. D. 6. 若关于的函数的定义域为,则实数的取值范围为() A. B. C. D. 7. 已知,,则() A. B. C. D. 8. 存在函数满足对于任意都有() A. B. C. D. 二、多选题(本题共3个小题,每小题6分,,在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有错选的得0分) 9. 下列说法正确的有() A. 的最小值为2 B. 最大值为 C. 的最小值为 D. 的最小值为2 10. ,则() A. B. C. D. 11. 已知定义在上的函数的图像关于中心对称,则下列说法一定正确的是() A. 若周期为2,则为奇函数 B. 为奇函数 C. 若周期为4,则为偶函数 D. 为奇函数 三、填空题:本题共3小题,每小题5分,,把答案直接填在答题卷中的横线上. 12. 已知角的终边过点,且,则角的弧度数是_____. 13. 已知函数,若的图象上存在不同的两个点关于原点对称,则实数的取值范围为_____. 14. 若存在(互不相等),满足,则的取值范围为_____. 四、解答题:本题共5小题,,解答应写出文字说明,证明过程或演算步骤. 15. 已知函数的定义域为A,函数,则的值域是B,不等式的解集为C. (1)求; (2)若,则实数a的取值范围. 16. 已知 (1)化简; (2)若,求的值: (3)若为第三象限角,且,求的值. 17. 已知函数是定义在上奇函数. (1)求实数的值; (2)若,不等式对恒成立,求实数得取值范围. 18. 已知函数,为常数. (1)证明:的图象关于直线对称. (2)设上有两个零点,. (ⅰ)求的取值范围; (ⅱ)证明:. 19. 已知函数,函数 (1)证明函数的奇偶性,并求的值; (2)判断函数在上的单调性,并利用定义法证明; (3),使在区间上的值域为,求实数的取值范围. 绵阳中学2024级高一上期选拔测试(数学) 一、单选题(本题共8个小题,每题5分,.在每个小题给出的四个选项中,只有一项是符合题目要求的) 1. 【答案】D 2. 【答案】C 3. 【答案】A 4. 【答案】D 5. 【答案】D 6. 【答案】C 7. 【答案】A 8. 【答案】D 二、多选题(本题共3个小题,每小题6分,,在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有错选的得0分) 9. 【答案】BC 10. 【答案】ACD 11. 【答案】AD 三、填空题:本题共3小题,每小题5分,,把答案直接填在答题卷中的横线上. 12.【答案】 13.【答案】 14. 【答案】 四、解答题:本题共5小题,,解答应写出文字说明,证明过程或演算步骤. 15. 【解】 【分析】(1)根据根式的意义求集合A,根据求集合B,进而求并集; (2)分、和三种情况解不等式求集合C,再结合即可得结果. 【小问1详解】 因为,解得或,即; 又因为,当且仅当时,等号成立,则, 可得,即; 所以. 【小问2详解】 对于不等式,令,可得或, 当时,则,可知不成立,不合题意; 当时,则,可知不成立,不合题意; 当时,则,若,则; 综上所述:实数a的取值范围为. 16. 【解】 【分析】(1)根据三角函数的诱导公式化简,从而得解; (2)利用(1)中结论,直接代入,结合三角函数的诱导公式即可得解; (3)根据题意,利用三角函数的诱导公式与基本关系式依次求得,从而得解. 【小问1详解】 . 【小问2详解】 因为, 所以. ... ...
~~ 已预览到文档结尾了 ~~