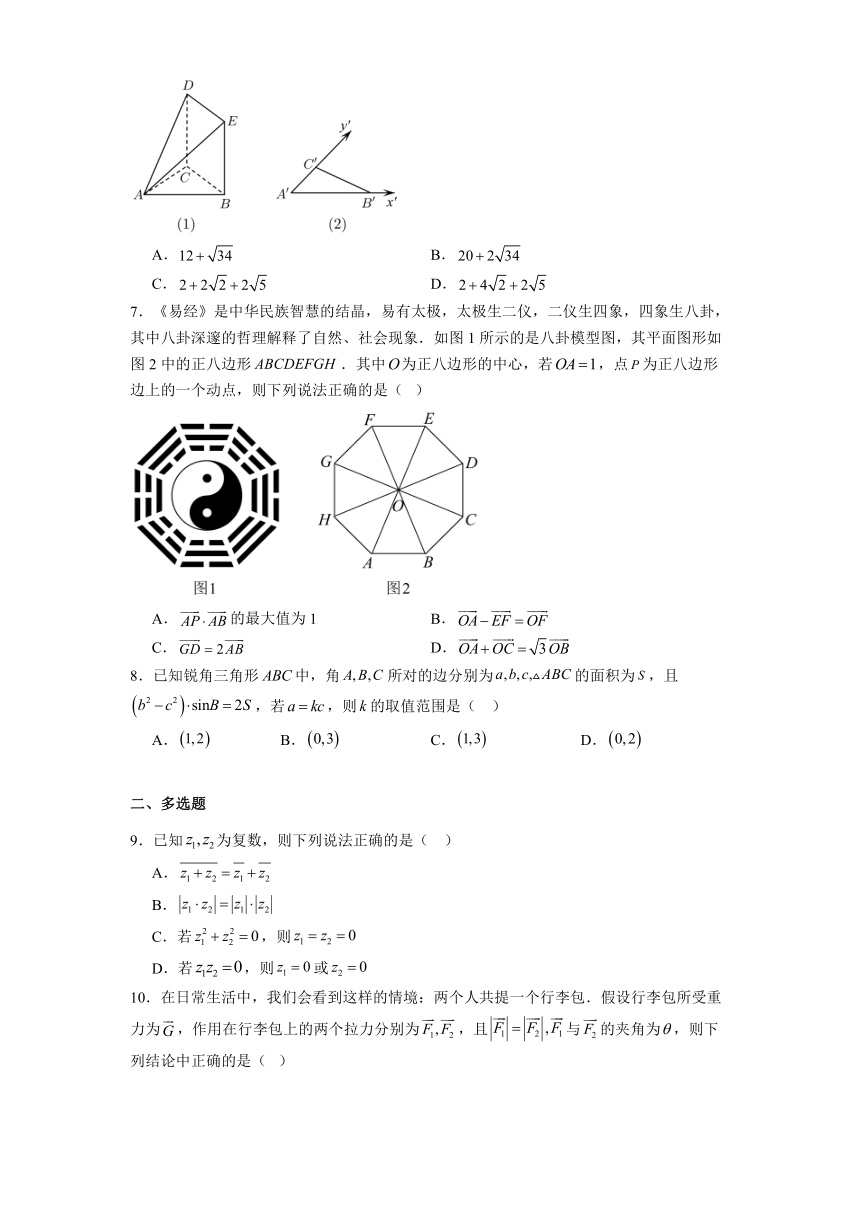
广东省东莞市五校2024?2025学年高一下学期联考数学试卷(含详解)

广东省东莞市五校2024 2025学年高一下学期联考数学试卷 一、单选题 1．从一个含有个个体的总体中抽取一容量为的样本，当选取抽签法、随机数法和分层随机抽样三种不同方法时，总体中每个个体被抽中的概率分别为，三者关系可能是（ ） A． B． C． D． 2．在复平面内，复数（其中i为虚数单位）的共轭复数对应的点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 3．在中，已知，则C＝（ ） A．60° B．30° C．30°或150° D．60°或120° 4．下面四个命题： ①过一点和一条直线垂直的直线有且只有一条； ②过一点和一个平面垂直的直线有且只有一条； ③过一点和一条直线垂直的平面有且只有一个； ④过一点和一个平面垂直的平面有且只有一个． 其中正确的是（ ） A．①④ B．②③ C．①② D．③④ 5．如图，在中，，点是的中点，设，则（ ） A． B． C． D． 6．在如图（1）所示的四棱锥中，底面为正方形，且侧面垂直于底面，水平放置的侧面的斜二测直观图如图（2）所示，已知，，则四棱锥的侧面积是（ ） A． B． C． D． 7．《易经》是中华民族智慧的结晶，易有太极，太极生二仪，二仪生四象，四象生八卦，其中八卦深邃的哲理解释了自然、社会现象．如图1所示的是八卦模型图，其平面图形如图2中的正八边形．其中为正八边形的中心，若，点为正八边形边上的一个动点，则下列说法正确的是（ ） A．的最大值为1 B． C． D． 8．已知锐角三角形中，角所对的边分别为的面积为，且，若，则的取值范围是（ ） A． B． C． D． 二、多选题 9．已知为复数，则下列说法正确的是（ ） A． B． C．若，则 D．若，则或 10．在日常生活中，我们会看到这样的情境：两个人共提一个行李包．假设行李包所受重力为，作用在行李包上的两个拉力分别为，且与的夹角为，则下列结论中正确的是（ ） A． B．越小越费力，越大越省力 C．当时， D．的范围为 11．如图，在棱长为1正方体中，点P，Q分别是线段，上的动点，点E是棱的中点，下列命题正确的有（ ） A．异面直线与所成的角为定值 B．的最小值为 C．三棱锥的体积随P点的变化而变化 D．过点E作平面，当//平面时，平面与正方体表面的交线构成平面多边形的周长为 三、填空题 12．已知单位向量满足，则 . 13．已知复数满足，当的虚部取最小值时， 14．农历五月初五是端午节.这一天民间有吃粽子的习俗，据说是为了纪念战国时期楚国大臣、爱国诗人屈原.粽子的形状有多种.今有某种粽子类似于由一个直角三角形绕它的一条直角边旋转（如图）而成.如果粽子的馅可以看成是这个几何体内的一个球状物，则粽子馅的最大体积为 . 四、解答题 15．已知复数，其中． （1）设，若是纯虚数，求实数m的值； （2）设，分别记复数在复平面上对应的点为A、B，求与的夹角余弦值以及在上的投影向量． 16．如图，在三棱锥中，． （1）平面； （2）当时，求二面角的正弦值． 17．在中，角，，的对边分别为，，，已知． （1）求角； （2）若，，求的面积． 18．已知正三棱柱中，点是的中点，底面的边长为2，． （1）求证：平面； （2）求三棱锥的体积； （3）求直线与平面所成角的正弦值． 19．在内一点满足，则称为的布洛卡点，为布洛卡角．小明同学对布洛卡点产生兴趣，对其进行探索得到许多正确的结论，比如，若下列问题中的点为的布洛卡点，请你和他一起解决如下问题： （1）当，且时，求； （2）角，，所对的边分别为，，，，求证：； （3）在（2）的条件下，若的周长为4，试把表示为的函数，并求的值域． 参考答案 1．【答案】B 【分析】根据抽样的概念，每个个体被抽中的概率是均等的，进而即可选择答案. 【详解】因为在抽签法抽样、随机数法抽样和分层随机抽样中，每个个体被抽中的概率均为， 所以. 故选B. 2 ... ...