
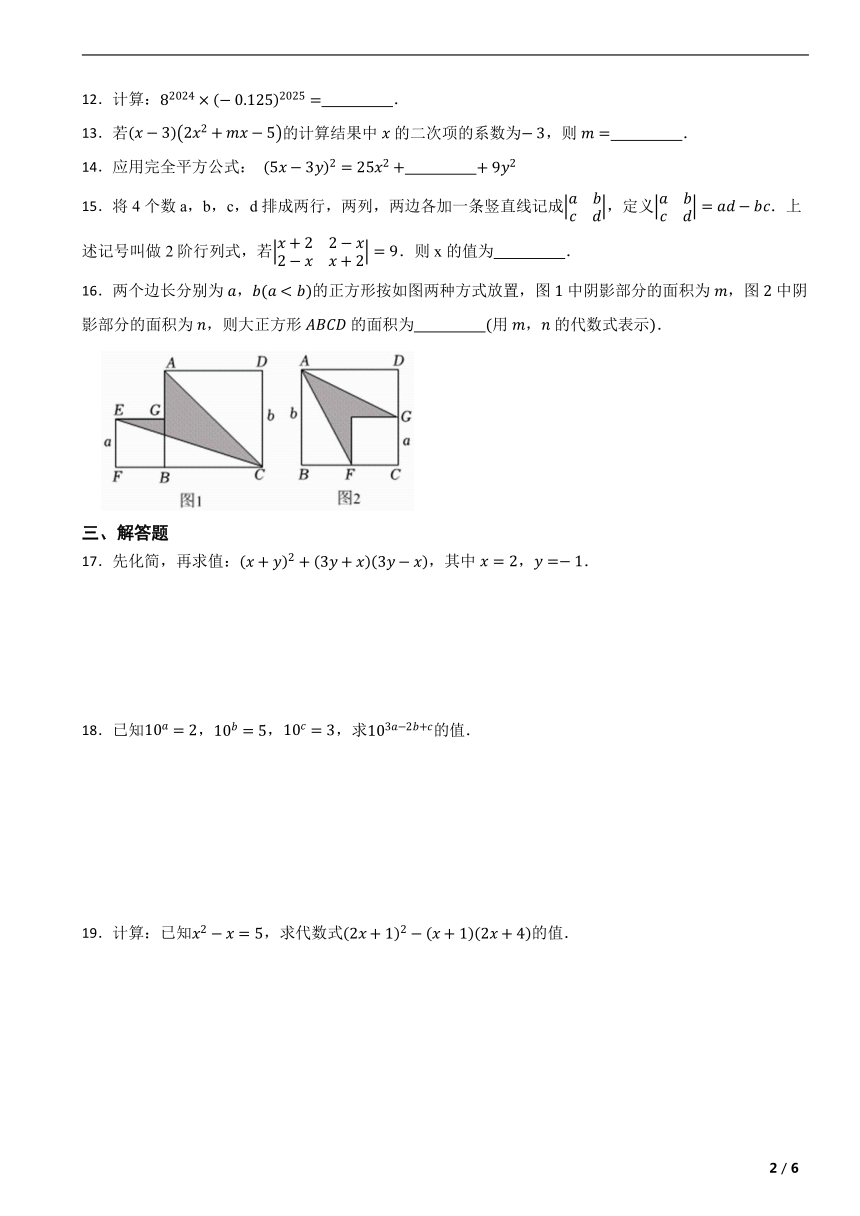
第三章 整式的乘除 一、选择题 1.下列计算正确的是( ) A. B. C. D. 2.已知一根头发的直径约为,数值0.0000007用科学记数法可表示为( ) A. B. C. D. 3.若,则■表示的运算符号为( ) A.+ B.- C. D. 4.下列多项式乘法能用平方差公式计算的是( ) A. B. C. D. 5.若与的乘积中不含的一次项,则的值为( ) A. B.3 C. D. 6.若,,且,则x的值是( ) A.1 B.2 C.3 D.4 7.计算结果正确的是( ) A. B. C. D. 8.若长方形的面积是,其中一边长是,则它的邻边长是( ) A. B. C. D. 9.计算的结果为( ) A. B. C. D. 10.长方形内,未被小长方形覆盖的部分用阴影表示,设左上角与右下角的阴影部分的面积的差为S,当的长度变化时,按照同样的方式放置,S始终不变,则a,b应满足( ) A. B. C. D. 二、填空题 11.计算: . 12.计算: . 13.若的计算结果中的二次项的系数为,则 . 14.应用完全平方公式: 15.将4个数a,b,c,d排成两行,两列,两边各加一条竖直线记成,定义.上述记号叫做2阶行列式,若.则x的值为 . 16.两个边长分别为,的正方形按如图两种方式放置,图中阴影部分的面积为,图中阴影部分的面积为,则大正方形的面积为 用,的代数式表示. 三、解答题 17.先化简,再求值:,其中,. 18.已知,,,求的值. 19.计算:已知,求代数式的值. 20.已知。 (1)化简; (2)若的值与的值无关,求的值。 21.已知x+y=5,xy=4. (1)求x2+y2的值; (2)求(x﹣y)的值. 22.【知识背景】在我国南宋数学家杨辉(约13世纪)所著回的《详解九章算术》(1261年)一书中,用如图的三角形解释二项和的乘方规律,法国数学家帕斯卡于1654年才发现此三角形,比中国晚了几百年,杨辉在注释中提到,在他之前北宋数学家贾宪(1050年左右)也用过这种方法,因此我们称这个三角形为“杨辉三角”或“贾宪三角”,此图揭示了(为非负整数)的展开式的项数及各项系数的有关规律: 【知识应用】 (1)补充完整的展开式,_____; (2)的展开式中共有_____项,所有项的系数和为_____; (3)今天是星期五,过了天后是星期几? 23.对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式.例如由图1可以得到,这样就用图形面积验证了完全平方公式. (1)类似的,写出图2中所表示的数学等式为_____; (2)如图3,用不同的代数式表示大正方形的面积,由此得到的数学等式为_____; (3)利用上面(2)的结论解决问题:若,求的值; (4)利用此方法也可以求出一些不规则图形的面积.如图4,将两个边长分别为和的正方形拼在一起,三点在同一直线上,连接和,若这两个正方形的边长满足,,请求出阴影部分的面积. 参考答案 1.C 2.D 3.D 4.B 5.A 6.C 7.B 8.D 9.C 10.B 11. 12. 13. 14. 15. 16. 17.; 18. 19. 20.(1)解:当,=3xy+3y-2。 (2)解:方法一:∵A-2B=3xy+3y-2,且与y的值无关, ∴3x+3=0,∴x=-1。 当x=-1时,A-2B=-3y+3y-2=-2, ∴2A-4B=2×(A-2B)=2×(-2)=-4。 方法二:∵A-2B=3xy+3y-2,且与y的值无关, ∴3x+3=0, ∴x=-1。 2A-4B=2(2x2+xy+3y)-4(x2-xy+1) =4x2+2xy+6y-4x2+4xy-4 =6xy+6y-4。 当x=-1时,2A-4B=6xy+6y-4=-6y+6y-4=-4。 方法三:∵A-2B=3xy+3y-2,且与y的值无关, ∴3x+3=0, ∴A-2B=-2, ∴2A-4B=2(A-2B)=2×(-2)=-4。 21.(1) (2) 22.(1)6,4, (2)8, (3)星期六 23.(1) (2) (3) (4) 1 / 1 ... ...
~~ 已预览到文档结尾了 ~~