
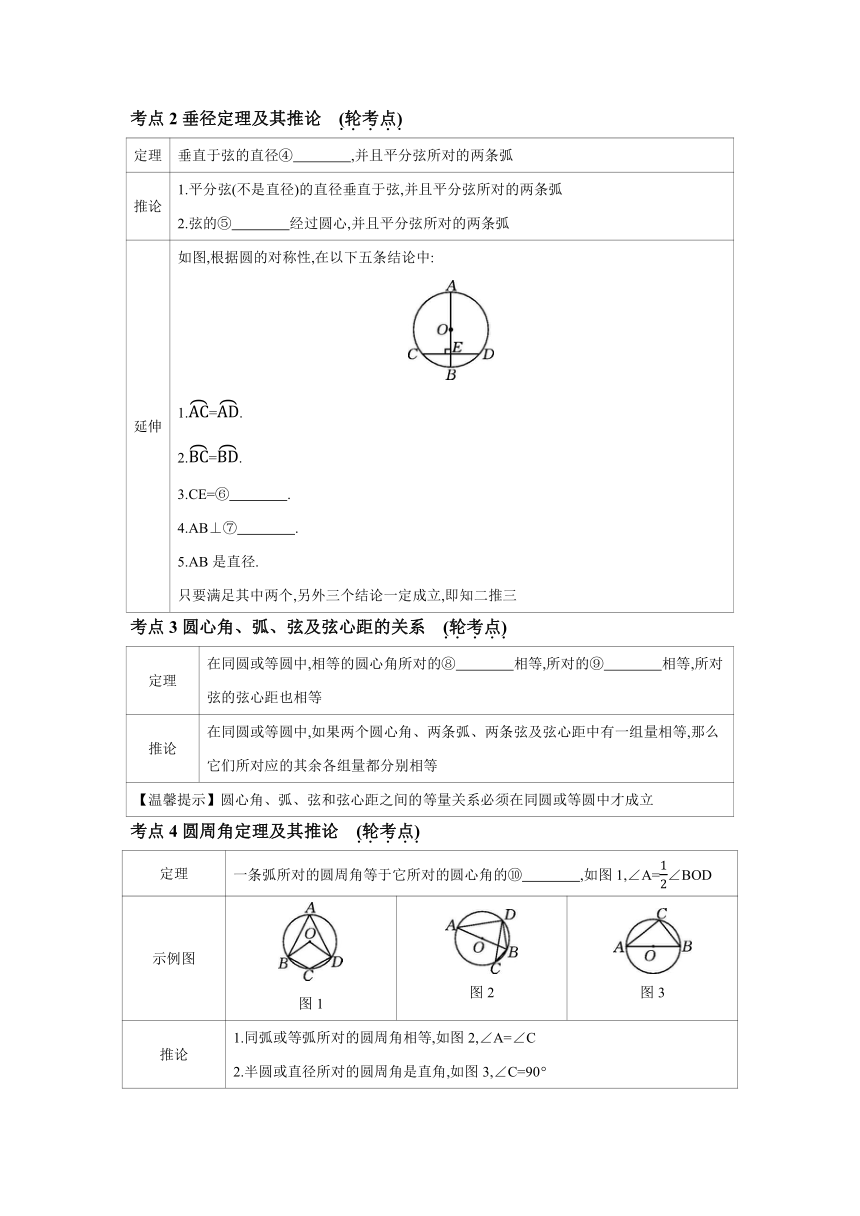
第1节 圆的基本性质 (6年3考,2分) 圆的基本性质的考查多以圆周角定理,垂径定理和弧、弦、圆心角之间的关系为主,一般以选择题和填空题的形式出现,也有一些简单的解答题,复习时一是要熟练掌握圆的相关定理和性质,二是要强化训练常考题型,举一反三.但随着新课程标准将垂径定理作为必学内容这一变化的出现,2023年和2024年在解答题中进行了重点考查,预测2025年的中考试题会更多体现新课标的理念. 回归教材·过基�———河北中考核心考点梳理 【知识体系】 【考点清单】 考点1圆的有关概念 (轮考点) 定义 几何定义:圆是平面上到定点(圆心)的距离等于定长(半径)的点的集合,如图所示的圆记为☉O 旋转定义:圆也可以看作是一条线段绕其固定的一端点(圆心)旋转一周,其另一端点所描绘出的轨迹 弦与直径 连接圆上任意两点的线段(线段AD)叫作弦,过圆心的弦叫作直径(线段AB),直径是圆内① 的弦 弧 圆上任意两点间的部分叫作弧,小于半圆的弧叫② (如),大于半圆的弧叫③ (如) 等弧 同圆或等圆中,能够互相重合的弧 圆心角 顶点在圆心的角(如∠AOC) 圆周角 顶点在圆上,并且两边都与圆相交的角(如∠ADC) 弦心距 圆心到弦的距离(线段OE的长) 考点2垂径定理及其推论 (轮考点) 定理 垂直于弦的直径④ ,并且平分弦所对的两条弧 推论 1.平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧 2.弦的⑤ 经过圆心,并且平分弦所对的两条弧 延伸 如图,根据圆的对称性,在以下五条结论中: 1.=. 2.=. 3.CE=⑥ . 4.AB⊥⑦ . 5.AB是直径. 只要满足其中两个,另外三个结论一定成立,即知二推三 考点3圆心角、弧、弦及弦心距的关系 (轮考点) 定理 在同圆或等圆中,相等的圆心角所对的⑧ 相等,所对的⑨ 相等,所对弦的弦心距也相等 推论 在同圆或等圆中,如果两个圆心角、两条弧、两条弦及弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等 【温馨提示】圆心角、弧、弦和弦心距之间的等量关系必须在同圆或等圆中才成立 考点4圆周角定理及其推论 (轮考点) 定理 一条弧所对的圆周角等于它所对的圆心角的⑩ ,如图1,∠A=∠BOD 示例图 图1 图2 图3 推论 1.同弧或等弧所对的圆周角相等,如图2,∠A=∠C 2.半圆或直径所对的圆周角是直角,如图3,∠C=90° 圆内接四边形 圆内接四边形的对角互补,如图1,∠A+∠C=180°,∠ABC+∠ADC=180° 【基础演练】 1.下列说法中,正确的是 ( ) A.过圆心的直线是圆的直径 B.直径是圆中最长的弦 C.相等长度的两条弧是等弧 D.顶点在圆上的角是圆周角 2.(北师九下P80随堂练习第1题变式)如图,AB是☉O的直径, ∠D=32°,则∠AOC等于 ( ) A.158° B.58° C.64° D.116° 3.如图,OA,OB,OC都是☉O的半径,AC,OB交于点D.若AD=CD=8,OD=6,则BD的长为 ( ) A.5 B.4 C.3 D.2 4.如图,将一个纵截面为半圆的容器水平放置,然后向其中倒入部分液体,测得数据如图所示(单位:cm),则液面宽度AB的长为 ( ) A.8 cm B.4 cm C.4 cm D.8 cm 5.如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为 ( ) A.3 B.4 C.5 D.6 6.(冀教九上P158习题第2题变式)如图,在☉O中,AB为直径,C为圆上一点,∠BAC的平分线与☉O交于点D,若∠ADC=20°,则∠BAD= °. 7.如图,在☉O中,四边形OABC为菱形,点D在上,则∠ADC的度数是 . 真题精粹·重变式———河北6年真题精选及拓展 考向1圆周角定理及垂径定理 (6年6考) 1.(2021·河北16题2分)如图,在等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作: ①以O为圆心,OA为半径画圆; ②在☉O上任取一点P(不与点A,B重合),连接AP; ③作AB的垂直平分线与☉O交于M,N两点; ④作AP的垂直平分线与☉O交于E,F ... ...
~~ 已预览到文档结尾了 ~~