
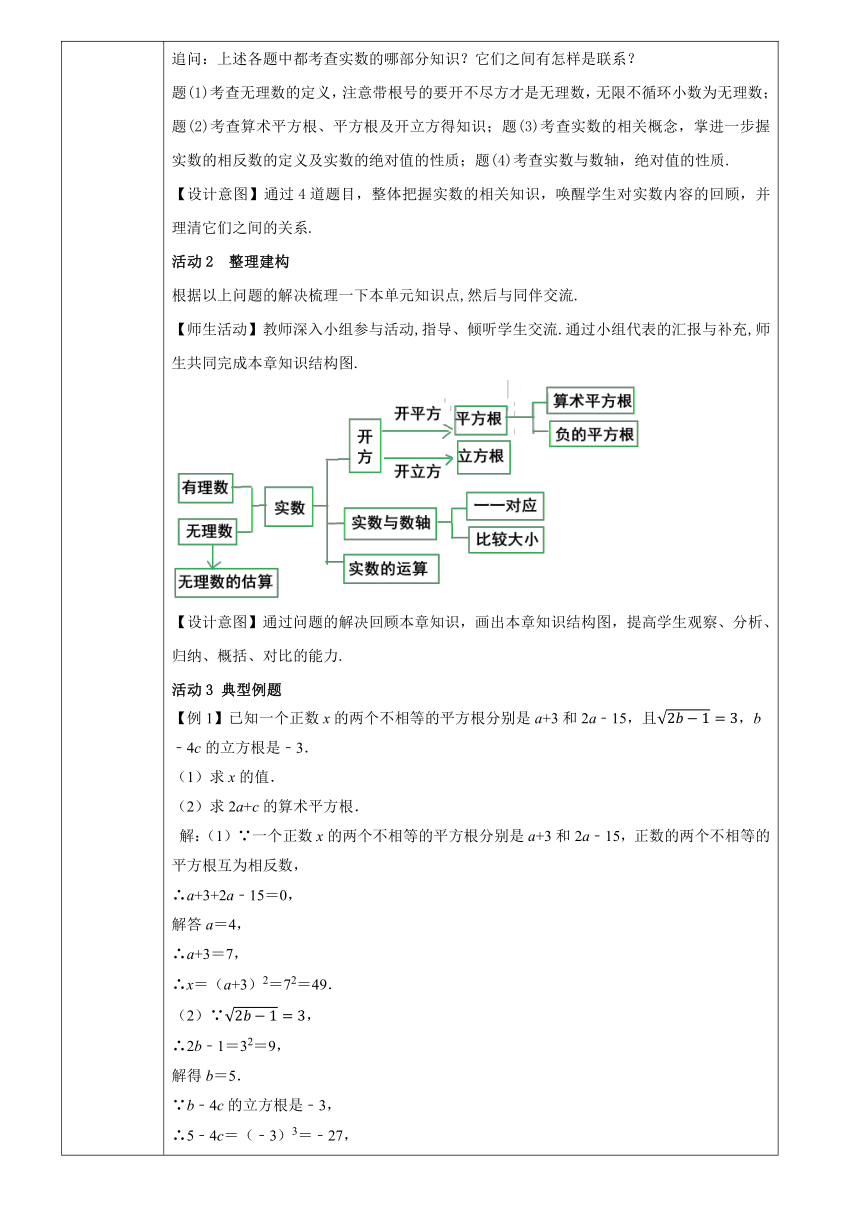
第四章 实数 本章考点复习 教学设计 教学目标 1.掌握实数的有关概念、表示方法、并运用性质进行相关的计算. 2.会判断一个数是不是无理数、会估算一个无理数的大致范围. 3.会利用估算的方法比较两个无理数的大小,根据精确度的要求进行无理数的近似计算。 教学重难点 重点:复习有理数的相关计算 难点:建立本章知识结构 教学策略 首先通过问题引入,回顾本单元的基础知识,并构建出知识网络图,从而理解各知识点间的联系,再通过基础题目训练,对基本解题方法做一个梳理.在学生把握基本内容的基础上,教师引导学生进一步提炼,在此基础上解决典型例题.通过学生尝试解决问题,以及师生之间、生生之间的讨论交流,使学生对数学思想方法的认识更深刻,对解决问题的策略把握得更灵活. 教学过程 教学步骤 教学活动 情境导入 我们学习了实数的相关知识及运算,大家对本章内容掌握得怎样?还有哪些需要巩固的知识点?通过这一节课的复习,希望大家有进一步的认识与收获. 【设计意图】直接点出本节课的学习目标,激发学生的学习的兴趣,调动学习积极性. 复习巩固 活动1 复习回顾 1.在数﹣65,,3.14,0,,﹣π,0.020020002…中,无理数共有 个. 2.的算术平方根是 ; ;的平方根是 . 3.的相反数是 ;绝对值等于的数是 . 4.已知实数a、b在数轴上的对应点如图,化简|a|﹣|a+b|+|c﹣b|= . 【师生活动】学生先独立思考每个问题后在小组内交流,教师深入小组,并参与小组活动,及时了解学生对问题的掌握情况,对出现的错误进行纠正. 1.2 2.4;﹣2;±2. 3.; 解析:∵实数a的相反数是﹣a, ∴的相反数是. ∵一个正实数的相反数是它本身,一个负实数的相反数是它的相反数, ∴绝对值等于的数是. 4.c解析:由图可知,a<0,a<b<0<c,且|a|>|b|, 所以,a+b<0,c﹣b>0, 所以|a|﹣|a+b|+|c﹣b|=﹣a+a+b+c﹣b=c。 追问:上述各题中都考查实数的哪部分知识?它们之间有怎样是联系? 题(1)考查无理数的定义,注意带根号的要开不尽方才是无理数,无限不循环小数为无理数;题(2)考查算术平方根、平方根及开立方得知识;题(3)考查实数的相关概念,掌进一步握实数的相反数的定义及实数的绝对值的性质;题(4)考查实数与数轴,绝对值的性质. 【设计意图】通过4道题目,整体把握实数的相关知识,唤醒学生对实数内容的回顾,并理清它们之间的关系. 活动2 整理建构 根据以上问题的解决梳理一下本单元知识点,然后与同伴交流. 【师生活动】教师深入小组参与活动,指导、倾听学生交流.通过小组代表的汇报与补充,师生共同完成本章知识结构图. 【设计意图】通过问题的解决回顾本章知识,画出本章知识结构图,提高学生观察、分析、归纳、概括、对比的能力. 活动3 典型例题 【例1】已知一个正数x的两个不相等的平方根分别是a+3和2a﹣15,且,b﹣4c的立方根是﹣3. (1)求x的值. (2)求2a+c的算术平方根. 解:(1)∵一个正数x的两个不相等的平方根分别是a+3和2a﹣15,正数的两个不相等的平方根互为相反数, ∴a+3+2a﹣15=0, 解答a=4, ∴a+3=7, ∴x=(a+3)2=72=49. (2)∵, ∴2b﹣1=32=9, 解得b=5. ∵b﹣4c的立方根是﹣3, ∴5﹣4c=(﹣3)3=﹣27, 解得c=8, ∴2a+c=2×4+8=16, ∴2a+c的算术平方根为. 【设计意图】通过对题目的解答,掌握实数中的平方根、立方根、算术平方根的相关知识 通过让学生对易错之处进行辨析,掌握平方根、立方根的性质,进一步熟悉法则. 【例2】阅读下面的文字,解答问题: 我们知道是无理数,无理数是无限不循环小数,因此不能将的小数部分全部写出来,于是小慧用1来表示的小数部分,你明白小慧的表示方法吗? 事实上,因为的整数部分是1,将一个 ... ...
~~ 已预览到文档结尾了 ~~